متوازي الأضلاع
- متوازي الأضلاع
- خواص متوازي الأضلاع
- خواص متوازي الأضلاع الخاصة
- مساحة متوازي الأضلاع
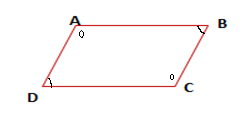
متوازي الأضلاع هو شكل رباعي، فيه كل ضلعين متقابلين متوازيان.
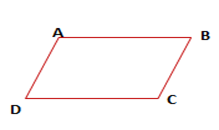
لدينا:
يتقاطع قطري متوازي الأضلاع في نقطة تمثل منتصف كل منهما.
- نقطة تقاطع القطرين هي مركز تناظر متوازي الأضلاع.
- قطري الرباعي متناصفين.
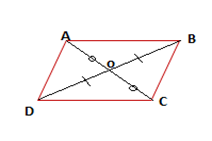
متوازي أضلاع إذن:
- هي منتصفأي:
- هي منتصفأي:
في متوازي الأضلاع، كل ضلعين متقابلين، لهما نفس الطول ومتوازيان.
- و
- و
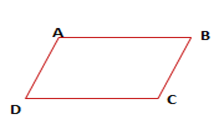
في متوازي الأضلاع كل زاويتين متقابلتين لهما نفس القيس.
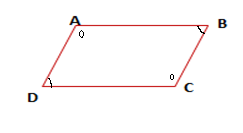
في متوازي الأضلاع كل زاويتين متتاليتين متكاملتان.
لإثبات أن رباعي يكون متوازي إضلاع يكفي أن تتحقق إحدى الشروط التالية:
- كل ضلعين متقابلين متوازيان.
- كل ضلعين متقابلين متقايسان.
- القطران متناصفان.
- كل زاويتان متقابلتين لهما نفس القيس.
- كل زاويتين متتاليتين متكاملتين.
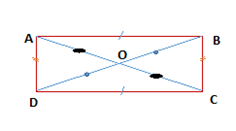
المستطيل هو متوازي أضلاع زواياه قائمة.
- زواياه الأربعة قائمة
- قطرا المستطيل متناصفان ومتقايسان منه:و
- نقطة تقاطع قطراه هي مركز تناظر المستطيل
- محاور تناظر المستطيل هما محاور أضلاعه
لإثبات أن رباعي هو مستطيل نتحقق من وجود إحدى الخواص السابقة .
المعين هو متوازي أضلاع له ضلعان متتليان متقايسان.
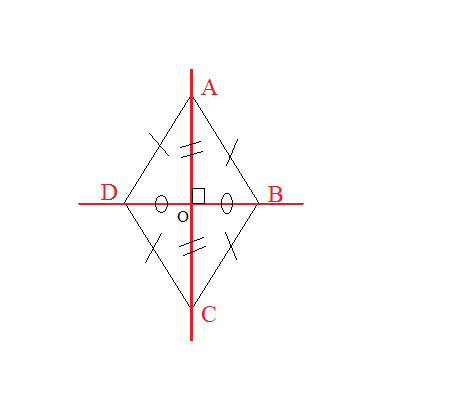
- قطرا المعين متعامدان . و متناصفان منه:و
- أطوال أضلاعه متساوية
- كل زاويتين متقابلتين لهما نفس القيس و
- مركز تناظر المعين هي نقطة تقاطع قطريه.
- محورا تناظر المعين هم قطراه
لإثبات أن رباعي هومعين يكفي توفر إحدى الخواص السابقة في المربع .
- ملاحظة:
تنطبق جميع خواص متوازي الأضلاع على المعين.
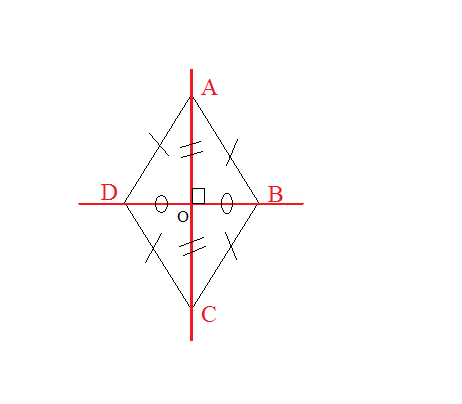
المربع هو متوازي أضلاع زواياه قائمة وأضلاعه متقايسة.
- زواياه الأربعة قائمة
- قطرا المربع متعامدان، متناصفان ومتقايسان
- قطرا المربع ينصفان زواياه
- مركز تناظر المربع هي نقطة تقاطع قطريه.
- محورا تناظر المربع هما قطراه أو محاور أضلاعه
لإثبات أن رباعي هو مربع يكفي توفر إحدى الخواص السابقة.
- ملاحظة:
تنطبق جميع خواص المعين و المستطيل على المربع.
مساحة متوازي الأضلاع هي جداء طول أحد أضلاعه والارتفاع المتعلق به :
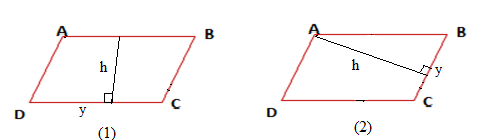
نعبر عن
- إختبارات
- 30
- الأجوبة الصحيحة
- False
- الأجوبة الخاطئة
- False
- مجموع النقاط
- False
المراتب الخمس الأولى في Quiz
- abderrahmane meddahi
- 5618 نقطة
-

- camellia benbrahim
- 1970 نقطة
-

- YASSINE BERKANI
- 528 نقطة
-

- zaki amr
- 252 نقطة
-

- Mehdi usma
- 221 نقطة
-

- hadjer BENMEBIROUK
- 220 نقطة
-

- RELECTURE relecture
- 220 نقطة
-

- الحمد لله
- 217 نقطة
-

- DINA AKSAS
- 200 نقطة
-

- sirina sisita
- 200 نقطة
-










