المثلثات : حالات تقايس المثلثات – المستقيمات الخاصة في مثلث
مثلثان متقايسان هما مثلثان قابلان للتطابق .
يتقايس مثلثان اذا تقايس فيهما ضلعان و الزاوية المحصورة بينهما.
لدينا:
ومنه:
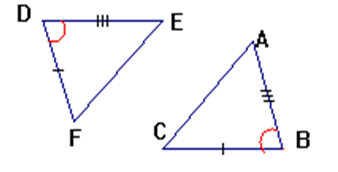
يتقايس مثلثان اذا تقايس فيهما زاويتان و الضلع المحصور بينهما .
لدينا:
ومنه:
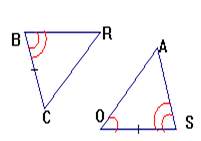
يتقايس مثلثان اذا تقايست فيهما الأضلاع الثلاثة
لدينا:
و منه:
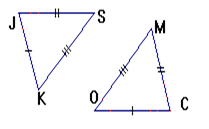
يتقايس مثلثان قائمان اذا تقايس فيهما الوتر و ضلع قائم .
و منه:
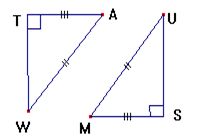
يتقايس مثلثان قائمان اذا تقايس فيهما الوتر و زاوية حادة .
لدينا:
ومنه:
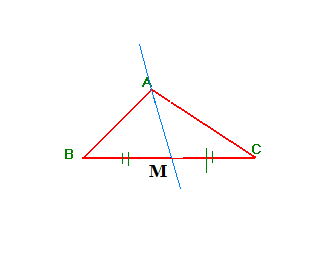
محور ضلع في مثلث هو المستقيم العمودي على هذا الضلع في منتصه.
في المثلث
و منه:
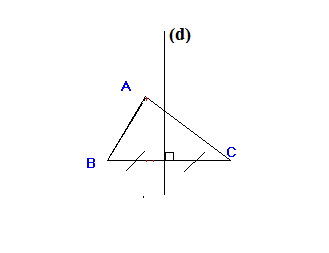
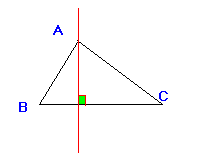
- المحاور الثلاث لمثلث تتقاطع في نقطة واحدة تسمى نقطة تلاقي المحاور .
- إذا كان لمثلث زاوية منفرجة فإن نقطة تلاقي محاوره تقع خارج المثلث.
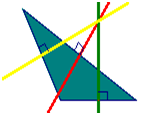
الارتفاع المتعلق بضلع في مثلث هو المستقيم العمودي على هذا الضلع و الذي يشمل الرأس المقابل له .
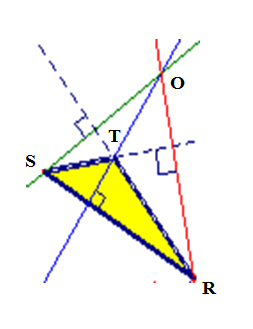
- باستعمال الادوات الهندسية المناسبة و بطريقتين مختلفتين أنشئ محور الضلع [SR].
- باستعمال الادوات الهندسية المناسبة انشئ الارتفاعات المتعلقة بأضلاع المثلث السابق
ملاحظة : التركيز يكون على صحة وحسن استعمال الادوات الهندسية في الانشاء
الارتفاعات الثلاثة في مثلث تتقاطع في نقطة واحدة تسمى نقطة تلاقي الارتفاعات .
المتوسط المتعلق بضلع في مثلث هو مستقيم يشمل الرأس المقابل لهذا الضلع و منتصف هذا الضلع .
في المثلث
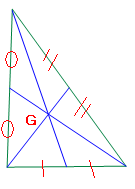
في مثلث المتوسطات تتقاطع في نقطة واحدة تسمى نقطة تلاقي المتوسطات .
في هدا المثلث تقاطعت المتوسطات في نقطة واحدة
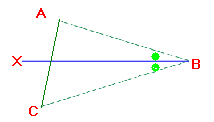
منصف زاوية في مثلث هو نصف المستقيم الذي يشمل رأس الزاوية و يجزئها الى زاويتين متقايستين .
في المثلث
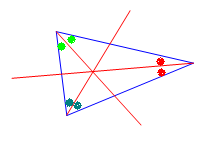
منصفات زوايا مثلث تتقاطع في نقطة واحدة تسمى نقطة تلاقي المنصفات
في مثلث تتقاطعت المنصفات في نقطة واحدة تسمى نقطة تلاقي المنصفات .
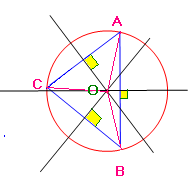
نقطة تلاقي محاور مثلث هي مركز الدائرة المحيطة بهذا المثلث .
ملاحظة :لتحديد مركز الدائرة المحيطة بمثلث يكفي إنشاء محورين فقط .
الدائرة محيطة بالمثلث
كل نقطة تنتمي الى منصف زاوية هي متساوية البعد عن ضلعي هذه الزاوية .
كل نقطة متساوية البعد عن ضلعي زاوية , تكون تنتمي الى منصف هذه الزاوية .
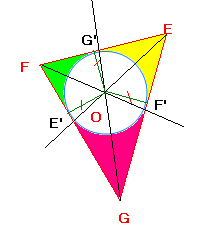
نقطة تلاقي منصفات زوايا مثلث هي مركز للدائرة المرسومة بداخله (التي تمس أضلاعه من الداخل ).
ملاحظة: لتحديد مركز الدائرة المرسومة داخل مثلث يكفي إنشاء منصفي زاويتين فقط .
الدائرة محيطة بالمثلث
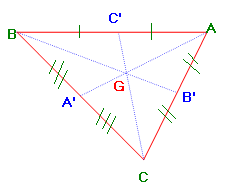
المتوسطات الثلاثة في مثلث تتلاقى في نقطة واحدة تسمى مركز ثقل المثلث و تقع في ثلثي كل متوسط ابتداءا من الرأس المناسب لهذا المتوسط .
مركز ثقل
- إختبارات
- 20
- الأجوبة الصحيحة
- False
- الأجوبة الخاطئة
- False
- مجموع النقاط
- False
المراتب الخمس الأولى في Quiz
- انفال مشهود
- 337 نقطة
-

- منير نجاري
- 262 نقطة
-

- رامي خرباش
- 262 نقطة
-

- nada djoudi
- 240 نقطة
-

- abdelbasat askiou
- 218 نقطة
-

- Bayou Liamine
- 200 نقطة
-
- ikram tahagaies
- 200 نقطة
-

- fafi ritaj
- 200 نقطة
-

- بن موسى محمد يونس
- 193 نقطة
-

- soraya bireche
- 192 نقطة
-










