النسب المثلثية في المثلث القائم
جب (sinus) الزاوية الحادة يساوي النسبة :
جيب تمام (cosinus) زاوية حادة يساوي النسبة:
ظل (tangante) زاوية حادة يساوي النسبة :
- نسمي في المثلث القائم الضلع المقابل للزاوية القائمة وترا .
- جب و جيب تمام زاوية حادة محصورة بين 0 و 1 .
- ظل أي زاوية حادة هو عدد حقيقي موجب .
لحساب جيب زاوية x علم قيسها بالدرجة ٬ نتبع الخطوات التالية ابتداءا من اليسار
= ; ادخال قيمة MODE ; DRG ; SIN ; X
اذا تعلق الأمر بحساب جيب تمام x أو ظل x نختار اللمسة COS أو TAN
أحسب
°SIN 36 ننفذ البرنامج ( من اليسار الى اليمين ) يظهر : ...0,587 = °SIN 36
لحساب القيس x بالدرجة لزاوية علم جيب هذه الزاوية ٬ باستعمال حاسبة ٬ ننفذ البرنامج التالي :
في بعض الحاسبات اللمسة 2nd تعوض باللمسة SHIFT
نختار اللمس
حدد قيس الزاوية
SHIFT cos 0,5 و منه °x = 60
لانشاء هندسيا زاوية علمت القيمة المضبوطة لاحدى نسبها المثلثية نكتب النسبة المثلثية على شكل كسر .
- اذاكانت النسبة المثلثية هي جيب أو جيب تمام الزاوية ننشئ مثلثا قائما فان طول أحد ضلعي زاويته القائمة هو بسط الكسر و طول وتره هو مقامه .
- اذا كانت النسبة المثلثية هي ظل الزاوية نشئ مثلثا قائما فان طولا ضلعي زاويته القائمة هما بسط و مقام الكسر .
أنشئ دون الاستعانة بالمنقلة زاوية بحيث جيبها التمام هو
لدينا :
كلا من 5 و 4 يمثلان مقام و بسط النسبة
نبدأ بانشاء زاوية قائمة رأسها A ثم ننشأ B أحد ضلعي هذا المثلث بحيث :
ثم نرسم الدائرة التي نصف قطرها
النقطة C.
في المثلث القائم في A لدينا
في مثلث قائم من أجل كل عدد
RTS مثلث قائم في T حيث :
- أحسب الطول TR ثم عين مدوره الى 0,1 .
- أحسب TS بتدوير الى 0,1
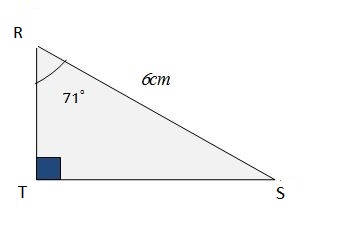
حساب TR :
بماأن TR ضلع يجاور الزاوية
اذن
حساب TS :
لدينا
اذن
DEF مثلث قائم في D حيث : DE = 3 cm و DF = 5 cm
- أحسب بالتدوير الى 0,01 قيس الزاوية ثم أستنتج قيس الزاوية
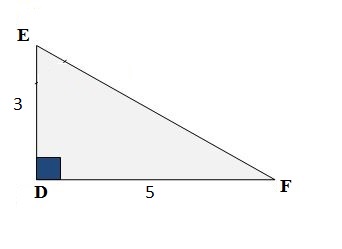
لدينا
اذن باستعمال
استنتاج قيس الزاوي
بماأن المثلث EFD قائم في D فان
و منه
- إختبارات
- 20
- الأجوبة الصحيحة
- False
- الأجوبة الخاطئة
- False
- مجموع النقاط
- False
المراتب الخمس الأولى في Quiz
- Marwan Kharroubi
- 528 نقطة
-

- نسرين فاطمة الزهراء صيدون
- 240 نقطة
-

- عبد النور بن قاسم
- 230 نقطة
-

- Amani BOUCHEBAK
- 220 نقطة
-

- Hîm Rã
- 217 نقطة
-
- وائل حسيني
- 200 نقطة
-

- imane sedrati
- 200 نقطة
-

- nounou arbouche
- 200 نقطة
-

- hammoud menigher
- 200 نقطة
-

- mohamed aymen mahi
- 200 نقطة
-










