المعادلات و المتراجحات من الدرجة الاولى بمجهول واحد
a , b , x أعداد حيث
نسمي معادلة من الدرجة الأولى بمجهول واحد x , كل معادلة يمكن كتابتها على الشكل
كل عبارة من العبارات الاتية هي معادلة من الدرجة الأولى بمجهول واحد :
حل المعادلة
حل المعادلتين :
- الحل:
من المعادلة
حل هده المعادلة : x = 2
من المعادلة
ومنه
المعادلة
- بعص المعادلات تكتب على شكل : و هي معادلات ليس لها حل .
- معادلات أخرى من الشكل : تقبل مالانهاية من الحلول (كل عدد هو حل لها)
- المعادلة : تكتب على الشكل
- المعادلة : صيغتها النهائيةاذن كل عدد هو حل لهذه المعادلة .
a , b , c , x أعداد .
نعلم أن الجداء ab يكون منعدما اذا كان أحد عامليه على الاقل معدوما 0 = ab يعني اما 0 = b و اما 0 = a
حلول المعادلة
لحل المعادلة :
- اما و منههو الحل الاول للمعادلة السابقة .
- و اما أيو منههو الحل الثاني .
المعادل من الشكل
لحل معادلة ليست من الدرجة الأولى نتبع مايلي .
- نجعل طرفها الأيمن صفرا .
- نحلل الطرف الأيسر الى جداء عاملين من الدرجة الأولى .
- نحل معادلة الجداء المعدوم ثم نستنتج حلول المعادلة المعطاة .
حل كلا من المعادلتين التاليتين :
- لحل المعادلة نكتبها على الشكل التالي
المعادلة
- لحل المعادلة نحوله الى الجداء المعدومو هي متطابقة تكتب على الشكل :
ترييض مسألة ( مشكل ) هو تحويلها من الأسلوب اللغوي الى الأسلوب الرياضي .
اب عمره 42 سنة و ابنه 12 سنة .
- بعد ثلاثة سنوات هل يصبح عمر الابن ثلث عمر الأب ؟
- لنكتب معادلة نبحث فيها بعد كم سنة يكون عمر الأب ضعف عمر الابن و نحسب سن كلا منهما .
- الحل :
بعد ثلاثة سنوات يصبح عمر الأب 45 سنة و سن ابنه 15 سنة و منه سيكون عمر الابن ثلث عمر ابيه .
نفرض x عدد السنوات التي فيها يصبح عمر الأب ضعف عمر الابن .و منه
و منه
نسمي متراجحة من الدرجة الأولى كل متراجحة من الشكل :
- المتراجحة تعني
أي
و منه
- المتراجحة تعني
أي
و منه
حل متراجحة هو ايجاد كل القيم الممكنة للمجهول التي تجعل المتباينة صحيحة .
هذه القيم تسمى حلول المتراجحة .
لنحل المتراجحتين السابقتين :
- بما أن تعني
فان
- بماأن تعني
فان
عندما نضرب أو نقسم طرفي متباينة في أو على عدد سالب و غير معدوم تتغير جهة المتباينة
(
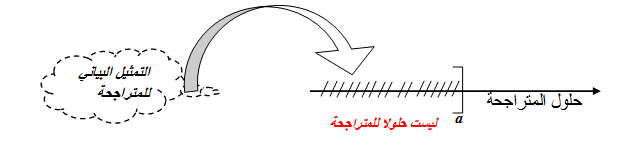
حلول المتراجحة
- إختبارات
- 20
- الأجوبة الصحيحة
- False
- الأجوبة الخاطئة
- False
- مجموع النقاط
- False
المراتب الخمس الأولى في Quiz
- Marwan Kharroubi
- 288 نقطة
-

- amel krim
- 222 نقطة
-

- مهدي نصر الدين
- 220 نقطة
-

- As Rayan
- 220 نقطة
-
- نسرين فاطمة الزهراء صيدون
- 220 نقطة
-

- أبوبكر بن عيسى
- 220 نقطة
-

- abd elkrim benyakhlef
- 217 نقطة
-

- yildirim cansu
- 200 نقطة
-

- rook mansour
- 200 نقطة
-

- اسيا بن عيشوش
- 200 نقطة
-










