الأعداد و الحساب
نسمي مجموعة الأعداد الحقيقية المجموعة التي نرمز إليها بالرمز

العدد 0 هي فاصلة النقطة O؛ العدد
نرمز إلى مجموعة الأعداد الحقيقية الموجبة بالرمز
العدد 0 ينتمي إلى المجموعتين معناه أن 0 عدد حقيقي موجب و سالب في نفس الوقت
نرمز إلى مجموعة الأعداد الحقيقية الغير معدومة بالرمز
نرمز إلى مجموعة الأعداد الطبيعية بالرمز
نرمز إلى مجموعة الأعداد الصحيحة النسبية بالرمز
نسمي عدد ناطق كل عدد يمكن كتابته على الشكل
نرمز إلى مجموعة الأعداد الناطقة بالرمز
نسمي عدد عشري كل عدد يمكن كتابته على الشكل
علما أن
نرمز إلى مجموعة الأعداد العشرية بالرمز
- نسمي عدد أصمّ كل عدد حقيقي ليس عدد ناطق
1) العدد 3 هو عدد طبيعي ؤ بالتالي ينتمي إلى مجموعة الأعداد الطبيعية
ونلخص ذالك بالكتابة :
و بما أن
و بما أن
و بالتالي ينتمي إلى مجموعة الأعداد الناطقة
ونلخص ذالك بالكتابة:
و بالتالي ينتمي إلى مجموعة الأعداد العشرية ونلخص ذالك بالكتابة:
2)
و بما أن
3)
4) ليست كل الأعداد الناطقة أعداد عشرية
العدد
5) توجد أعداد حقيقية ليست أعداد ناطقة، نذكر من بينها
تحقق المجموعات المذكورة في الأعلى الخاصية التالية :
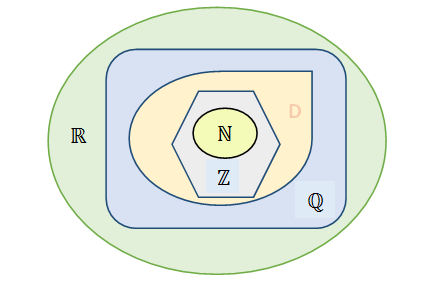
نقول عن العدد الناطق x حيث :
• الانتقال من الكتابة العشرية لعدد ناطق إلى الكتابة الكسرية
▪ لكل عدد ناطق كتابة عشرية تتضمن دورا
(سلسلة من أرقام تتكرر مالا نهاية من مرة)
و نختصر هذه الكتابة كمايلي
و نختصر هذه الكتابة كمايلي
و نختصر هذه الكتابة كمايلي
يمكن الانتقال من الكتابة العشرية لكل عدد ناطق إلى كتابته الكسرية باتباع الطريق التالية (نأخذ العدد كمثال )
- نكتب العدد الناطق على مجموع جزئيه الصحيح وجزئيه العشري
- نضع
و منه
و بما أن الدور يتكون من رقمين
- نحسب (100x) و سنجد
و منه (100x = 81 + 0.8181……………………………81)
معناه (100x = 81 + X) و منه
- نحل المعادلة ذات المجهول x و نجد
- نعوض في (1) و سنجد
و هي الكتابة الكسرية للعدد الناطق
a عدد حقيقي و n عدد طبيعي غير معدوم ، نسمي القوة النونية (أو القوة ذات الرتبة n ) للعدد الحقيقي a ، العدد الحقيقي
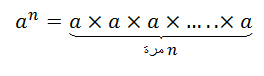
- و من أجل كل عدد حقيقي a و من أجل كل عدد طبيعي n غير معدوم :
نذقبل أن من أجل كل عدد حقيقي a :
من أجل كل عددين حقيقيين

- من أجل كل عدد حقيقي غير معدوم و من أجل كل عدد طبيعي غير معدوم n :
- إذا كان العدد الطبيعي n زوجي فإن و إذا كان n فردي فإن

نسمي الجذر التربيعي للعدد الحقيقي الموجب a ، العدد الحقيقي x الموجب حيث :
الجذر التربيعي للعدد 7 هو العدد الموجب x حيث
من أجل كل عدد حقيقي موجب a :
من أجل كل عددان حقيقيان موجبان a و b :
من أجل كل عددحقيقي موجب a ومن أجل كل عدد حقيقي موجب تماما b :
- إذا كان a و b عددان حقيقيان غير معدومان فإن :
- وومنه
- ومنه

ليكن عدد حقيقي x مكتوب على شكله العشري ،
وليكن a الرقم الذي يحتل الرتبة p و b
الرقم الذي يحتل الرتبة (p+1) في الجزء العشري من العدد x كما هو مبين في الجدول
نسمي مدوّر العدد x إلى العدد
- إذا كان الرقم نأخذ العدد x بنفس الجزء الصحيح و بكل أرقام جزئه العشري إلى غاية الرقم ذو الربة p و هو a
- إذا كان الرقم نأخذ العدد x بنفس الجزء الصحيح و بكل أرقام جزئه العشري إلى غاية الرقم ذو الربة p و هو a الذي يستبدل ب (a+1)
مدور العدد

بما أن الرقم الذي يأتي بعد الرقم الذي يحتل الرتبة الخامسة هو 2 و هو أصغر تماما من 5 فسنحتفظ بالرقم 9
مدور العدد

بما أن الرقم الذي يأتي بعد الرقم الذي يحتل الرتبة السادسة هو6 و هو أكبر من 5 فسنستبدل الرقم 2 ذو الرتبة السادسة ب 3
يمكن كتابة كل عدد عشري على الشكل:
الكتابة العلمية للعدد
الكتابة العلمية للعدد
لإزاحة الفاصلة نحو يسار العدد العشري ب n مرتبة نقسم هذا العدد على
لإزاحة الفاصلة نحو يمين العدد العشري ب n مرتبة نضرب هذا العدد ب
لإيجاد رتبة مقدار العدد الحقيقي x
1) نكتب العدد x على الشكل العلمي و نجد
2) ندور العدد العشري a إلى العدد الطبيعي الأقرب منه و نحتفظ بإشارة a و بقوة
بما أن
و بما أن مدور العدد 2.356 إلى الوحدة هو 2 فإن رتبة مقدار العدد 0.0002356 هي
نسمي عدد أولي كل عدد طبيعي الذي له بالضبط قاسمين مختلفين و في هذه الحالة القاسمين هما 1 و العدد الأولى نفسه
▪ 0 ليس عدد أولي لأن له عدد غير منتهي من القواسم و بالفعل كل الأعداد الطبيعية الغير معدومة تعتبر قواسم العدد 0
▪ 1 ليس عدد أولي لأن له قاسم واحد و هو 1
▪ 2 عدد أولي لأن له قاسمين لا أقل و لا أكثر و هما 1 و 2
لمعرفة هل العدد الطبيعي n عدد أولى أم لا نتبع الطريقة التالية
- نقسم هذا العدد على الأعداد الأولية حسب تسلسلها (يجب القيام بالقسمة الإقليدية معناه تعيين في كل مرة ما هو باقي القسمة) ثم
إما سنجد في مرحلة معينة باقي معدوم فنتوقف عن عمليات القسمة ونقول أن العدد n ليس عدد أولي
إما لا نجد باقي معدوم وسنتوقف عن عمليات القسمة عندما نجد حاصل القسمة أصغر من القاسم ونقول أن n أولي
1) هل العدد 511 عدد أولي؟
و منه العدد 511 ليس عدد أولي لأن له على الأقل أربعة قواسم :
1 ؛ 7 ؛ 73 ؛ ....؛ 511
2) هل العدد 2113 عدد أولي؟
و منه العدد 2113 عدد أولي
لتحليل العدد الطبيعي n إلى جداء عوامل أولية ينبغي أولا أن يكون هذا العدد ليس أولي ثم نتبع الطريقة التالية
- نقسم n على أصغر عدد أولي
- نقسم
نكرر هذه العمالية حتى نجد حاصل قسمة يساوي 1 وفي الأخير نجد
حيث
يمكن كتابة سلسلة عمليات القسمة على الشكل
و منه
- إختبارات
- 21
- الأجوبة الصحيحة
- False
- الأجوبة الخاطئة
- False
- مجموع النقاط
- False
المراتب الخمس الأولى في Quiz
- MED abdou
- 496 نقطة
-

- mohamed meddahi
- 432 نقطة
-

- رحمة بوعويش
- 349 نقطة
-

- ZAKARIA AB
- 265 نقطة
-

- khalil rafai
- 260 نقطة
-

- Bouizem Mehdi
- 260 نقطة
-
- war Fed
- 257 نقطة
-

- Draoui Abderrahim
- 240 نقطة
-
- sofian benchiker
- 240 نقطة
-

- كوثر زرادي
- 237 نقطة
-










