الترتيب -المجالات-القيمة المطلقة
a و b عددان حقيقيان
نقول أن a أصغر أو يساوي b إذا و فقط إذا
نقول أن a أكبر أو يساوي b إذا و فقط إذا
نقول أن a أصغرتماما من b إذا و فقط إذا
نقول أن a أكبر تماما من b إذا و فقط إذا
مقارنة بين العددين a و b هو تبيين من هي الجملة الصحيحة من بين الجمل:
نسمي الجمل
قارن بين
ومنه
ونكتب
مبرهنة : b ، a و c ثلاثة أعداد حقيقية
إذا كان
و نقول في هذه الحالة أن علاقة الترتيب علاقة متعدية
الدليل: إذا كان
و بما أن مجموع عددان سالبان عدد سالب فإن
و منه
إذا كانت
إذا كان
الدليل:
فإن
a ، b ، c ثلاثة أعداد حقيقية
- إذا كان فإن :تكافئ
- إذا كان فإن :تكافئ
الدليل :
- تكافئعدد سلب و بما أنفان (جداء عدد سلب بعدد موجب تماما نتيجته سالبة)
- تكافئعدد سلب و بما أنفان (جداء عدد سلب بعدد سالب تماما نتيجته موجبة)
إذا كانت c ، b ،a و d أعدادحقيقية موجبة
- إذا كان وفإن
- تكافئ
- تكافئ
الدليل: نعلم أن
- إذا كان فإنعدد سالب و إذا كانفإنعدد سالب و منه
- إذا كان فإن
- إذا كان فإنعدد سالب و منهعدد سالب و بما أنعدد موجب فإنعدد سالب و منه
- الخاصية تكافئتستنتج من الخاصيةتكافئ
مبرهنة:
إذا كان a وb عددان موجبان تماما فإن :
الدليل:
عندما تكون طرفي المتباينة سلبين معا، نضرب الطرفين باشارة سالبة ونغير إشارة المتباينة ونطبق الخواص المعطاة على الأعداد الموجبة
x و y عددان حقيقيان
- تكافيتكافي
- تكافيتكافي
- تكافيتكافئ
- تكافيتكافيتكافيتكافي
- إذا كان وتكافئوو منه
a و b عددان حقيقيان حيث
نسمي مجالا مغلقا حداه a وb ، مجموعة الأعداد الحقيقية x حيث :
ونمثل هذا المجال على المحور
حيث A هي النقطة التي فاصلتها a و B هي النقطة التي فاصلتها b
- مختلف أنواع المجالات :
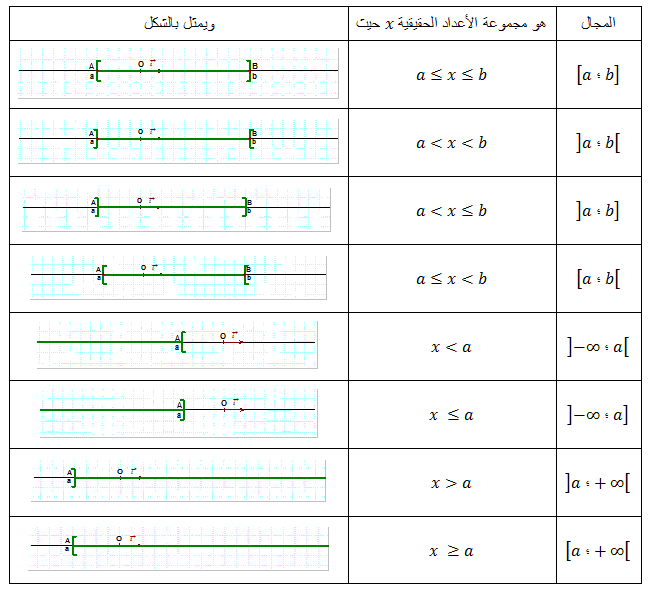
- تقاطع واتحاد مجالين
- نسمي تقاطع المجالين I و J المجال المتكون من الأعداد الحقيقية التي تنتمي إلى I او J
- نسمي اتحادالمجالين I و J المجالالمتكون من الأعداد الحقيقية التي تنتمي إلى I و J
نفرض أن
لإيجاد تقاطع أو أتحاد مجالين نلوّن المجالين بألوان مختلفة ثم نأخذ مجموعة النقط الملونة بللونين للتقاطع و نأخذ مجموعة النقط الملونة (مهما كان لونها ) للاتحاد
xعدد حقيقي و M نقطة من المستقيم
نسمي القيمة المطلقة للعدد x العدد الحقيقي الذي نرمز إليه ب:
و بما أن المسافة دائما موجبة فإن :
- إذا كان
- إذا كان
- لأنعدد موجب
- لأنعدد سالب
من أجل كل عدد حقيقي x و من أجل كل عدد حقيقي y :
- و إذا كان فإن
- إذا كان
▪ مبرهنة و تعريف
A و B نقطتين من المستقيم (D) المزود بالمعلم
فاصلتها a و b على هذا الترتيب
المسافة بين النقطتين A و B هي
ونسمي أيضا العدد |b-a|=|a-b| المسافة بين العددين a و b ونرمز إليها بالرمز
نسمي حصرا للعدد الحقيقي x كل مجال
و نسمي العدد
الحاسبة تعطي النتيجة التالية لما نضغط على
x عدد حقيقي كيفي و a عدد حقيقي موجب
الدليل
إذا كان
إذا كان
إذا كان
و منه
c عدد حقيقي كيفي،r عدد حقيقي موجب، من أجل كل عدد حقيقي x:
منه لما نضع
يمكن أن نعبر على نفس مجموعة الأعداد بقيمة مطلقة أو بمجال أو بحصر أو بمسافة باتباع الطريقة التالية
لما تعّرف المجوعة بالمجال [a ؛ b] نبحث عن cمركز المجال و r نصف قطره بالتعويض في
لما تعرف المجموعة بمسافة أو بقيمة مطلقة نستخرج و ثم نعوض في الجملة
نعتبر المجموعة المتكونة من الأعداد الحقيقية x حيث
و نبحث عن r نصف قطر المجال : نعلم أن

نعتبر الآن المجموعة المعرفة بالقيم المطلقة
نكتب القيمة المطلقة على الشكل
- إختبارات
- 22
- الأجوبة الصحيحة
- False
- الأجوبة الخاطئة
- False
- مجموع النقاط
- False
المراتب الخمس الأولى في Quiz
- MED abdou
- 417 نقطة
-

- ادم طلال بوسيف
- 354 نقطة
-

- رباب جعفري
- 269 نقطة
-

- anis krim
- 217 نقطة
-

- ALI ZOBIRI
- 200 نقطة
-

- Mokran Messaadi
- 200 نقطة
-

- ikram aissiou
- 200 نقطة
-

- Mouad Harrag
- 200 نقطة
-

- abdou abdou
- 200 نقطة
-

- adnan albi
- 200 نقطة
-










