الإحتمالات
- التجربة العشوائية
نسمي تجربة عشوائية كل تجربة لا يمكن توقع نتيجتها رغم معرفة كل نتائجها الممكنة
- إمكانية
نسمي إمكانية كل نتيجة ممكنة لتجربة عشوائية
نرمز بالرمز
- الحادثة
نسمي حادثة كل جزء من المجموعة الشاملة
المجموعة الخالية
المجموعة
المجموعة الجزئية المتكونة من إمكانية واحدة تدعي حادثة أولية
- الحادثة العكسية
نسمي الحادثة العكسية للحادثة A الحادثة التي نرمز إليها ب
- تقاطع حادثتين
نسمي تقاطع الحادثتين A وB الحادثة (A و B) التي نرمز إليها ب
- الحادثتين الغير متلائمتين
A و B حادثتين غير متلائمتين إذا و فقط إذا كانت الحادثة
- اتحاد حادثتين
نسمي اتحاد الحادثتين A وB الحادثة (A أو B) التي نرمز إليها ب
" رمي نردا ذو أربعة أوجه متقايسة وتحمل الأرقام: 1؛ 2؛ 3؛ 4 " تجربة عشوائية (نهتم برقم الوجه الذي سيكون قاعدته بعد الرمية معناه رقم الوجه الخافي)
المجموعة الشاملة هي
"الحصول على الرقم 1 " تعتبر إمكانية أو نتيجة ممكنة و الحادثة
الحادثة A : " الحصول على رقم زوجي " هي الحادثة
الحادثة العكسية للحادثة A هي الحادثة
الحاثة B : " الحصول على رقما أصغر أو يساوي 3 " هي
اتحاد الحادثتين A و B هي الحادثة (A أو B ) و هي :
نلاحظ أن
تقاطع المجموعتين A و B هي الحادثة (A و B ) و هي
الحادثة D :" الحصول على رقم أكبر أو يساوي 5 " حادثة مستحيلة لأن لا توجد أي إمكانية تحققها و منه
تعريف قانون الاحتمال على
احتمال الإمكانية
و منه :
▪ من أجل كل عدد طبيعي
بما أن كل القيم
حتميا أصغر أو يساوي 1
نقول عن تجربة عشوائية أنها متساوية الاحتمال إذا و فقط إذا كانت حوادثها الأولية لها نفس الاحتمال
و هذا معناه أن : من كل عددين طبيعيين
- النتيجة الأولى:
إذا كان المجموعة الشاملة
من أجل كل عدد طبيعي
نعلم أن
- النتيجة الثانية :
إذا كانت A حادثة محقق من أجل من أجل
و نكتب
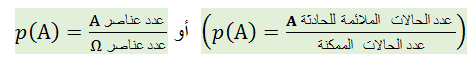
إذا كانت
- 1- من أجل كل حادثة A :
- 2- و
- 3- من أجل كل حادثتين A و B :
▪ إذا كانت A و B غير متلائمتين (معناه
من أجل كل حادثة A :
نرجع إلى مثال السابق
" رمي نردا ذو أربعة أوجه متقايسة وتحمل الأرقام: 1؛ 2؛ 3؛ 4 " تجربة عشوائية ( نهتم برقم الوجه الذي سيكون قاعدته بعد الرمية معناه رقم الوجه الخافي )
المجموعة الشاملة هي
الحادثة A : " الحصول على رقم زوجي " هي الحادثة
الحادثة العكسية للحادثة A هي الحادثة
الحاثة B : " الحصول على رقما أصغر أو يساوي 3 " هي
اتحاد الحادثتين A و B هي الحادثة (A أو B ) و هي :
تقاطع المجموعتين A و B هي الحادثة (A و B ) و هي
الحادثة D :" الحصول على رقم أكبر أو يساوي 5 " حادثة مستحيلة لأن لا توجد أي إمكانية تحققها و منه
إذا كانت
- الأمل الرياضي لقانون الاحتمال هو العددحيث
- تباين الاحتمال هو العددحيث :أومعناه
- الانحراف المعياري لقانون الاحتمال هو العدد الحقيقيحيث
نسمي متغيرا عشوائيا كل دالة عددية معرفة على
نرمي نردا مرة أولى و نسجل الرقم
نعتبر المغير العشوائي
المتغير العشوائي
و لتكن
نسمي قانون الاحتمال المتغير العشوائي
في المثال السابق قمنا برمي نردا مرة أولى و نسجل الرقم
نعتبر المغير العشوائي
و منه مجموعة قيم المتغير
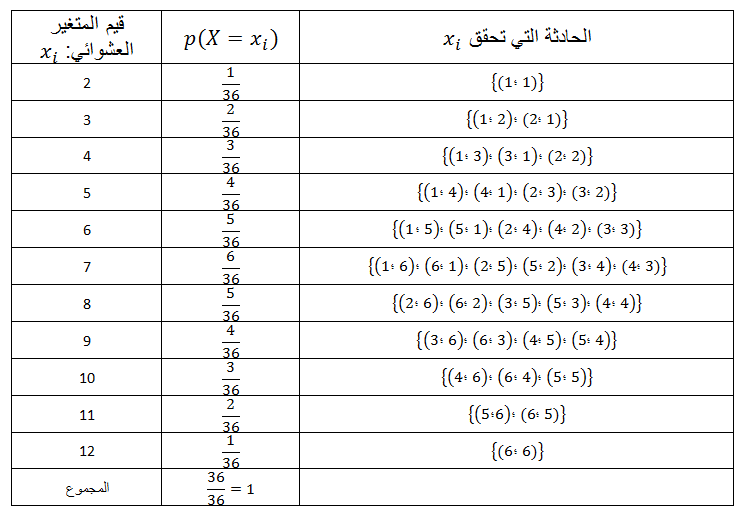
- نسمي الأمل الرياضي للمتغير العشوائي العدد الحقيقيحيث
- تباين المتغير العشوائي هو العددحيث :أو
- الانحراف المعياري للمتغير العشوائي هو العدد الحقيقيحيث
- إختبارات
- 21
- الأجوبة الصحيحة
- False
- الأجوبة الخاطئة
- False
- مجموع النقاط
- False
المراتب الخمس الأولى في Quiz
- LI Ght
- 258 نقطة
-

- souad otmani
- 155 نقطة
-

- Queen W
- 154 نقطة
-

- abderrahmen ham
- 154 نقطة
-

- dounya amrouche
- 154 نقطة
-

- sami asrir
- 154 نقطة
-

- ouranader hiba
- 153 نقطة
-

- nihed chouadra
- 144 نقطة
-

- amel hasbellaoui
- 137 نقطة
-

- abdelrahmane haddad
- 137 نقطة
-










