النهايات
نقبل دون برهان المبرهنات التالية:

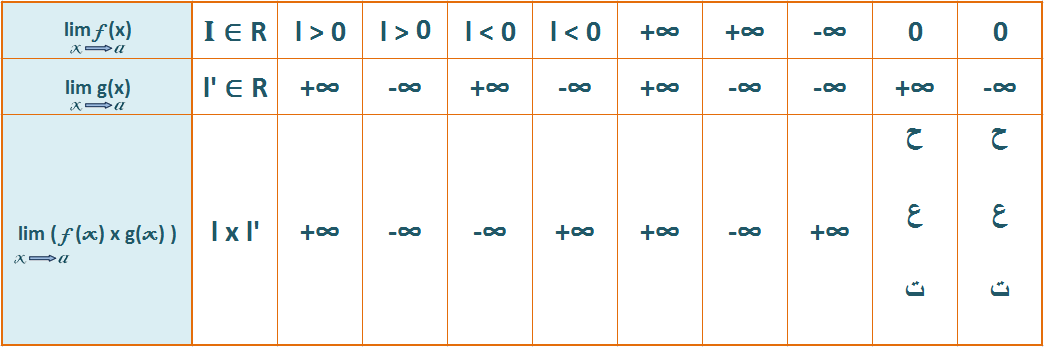
تسمى الحالات التي لا تسمح فيها النظريات السابقة من استنتاج النهاية بحالات "عدم التعيين" (ح ع ت)
قواعد إجرائية :
- النهاية لدالة كثير حدود عند وهي نهاية حدها الأعلى درجة عندو
- النهاية لدالة ناطقة عند وهي نهاية حاصل قسمة الحدين العلى درجة عندو عند
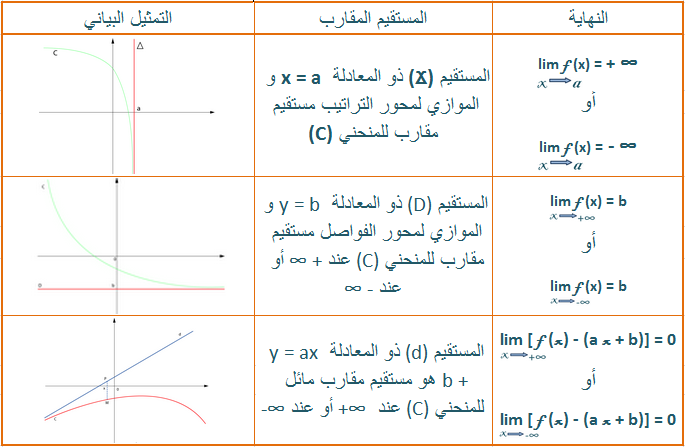
إذا كانت الدالة
لتكن
- تحقق أنه من أجل كل من:
- أحسب نهايات الدالة عند حدود
- عين المستقيمات المقاربة للمنحنى الممثل للدالة
- بتوحيد المقامات نحصل على:
بما أن
بما أن
بما أن
بما أن
- بما أن
فإن المنحنى
لدينا:
إذن المنحنى
إذا كان من أجل كل
و كانت
تبقى هذه النظرية صحيحة إذا كان
لدينا:
- إذا كان من أجل كل من:و كانتفإن
- إذا كان من أجل كل من:و كانتفإن
تبقى النتيجة صحيحة لما
- عين
لدينا:
تمثل أعداد حقيقية أو
إذا كانت
نعتبر الدالة
لنحسب
نلاحظ أن الدالة
بماأن
فإن:









