الدوال الأسية
دالة اللوغاريتم النيبيري مستمرة و متزايدة تماما على
و لدينا :
إذن حسب نظرية القيم المتوسطة ، من أجل كل عدد حقيقي
نكون قد عرّفنا هكذا دالة جديدة
رسم المنحنى
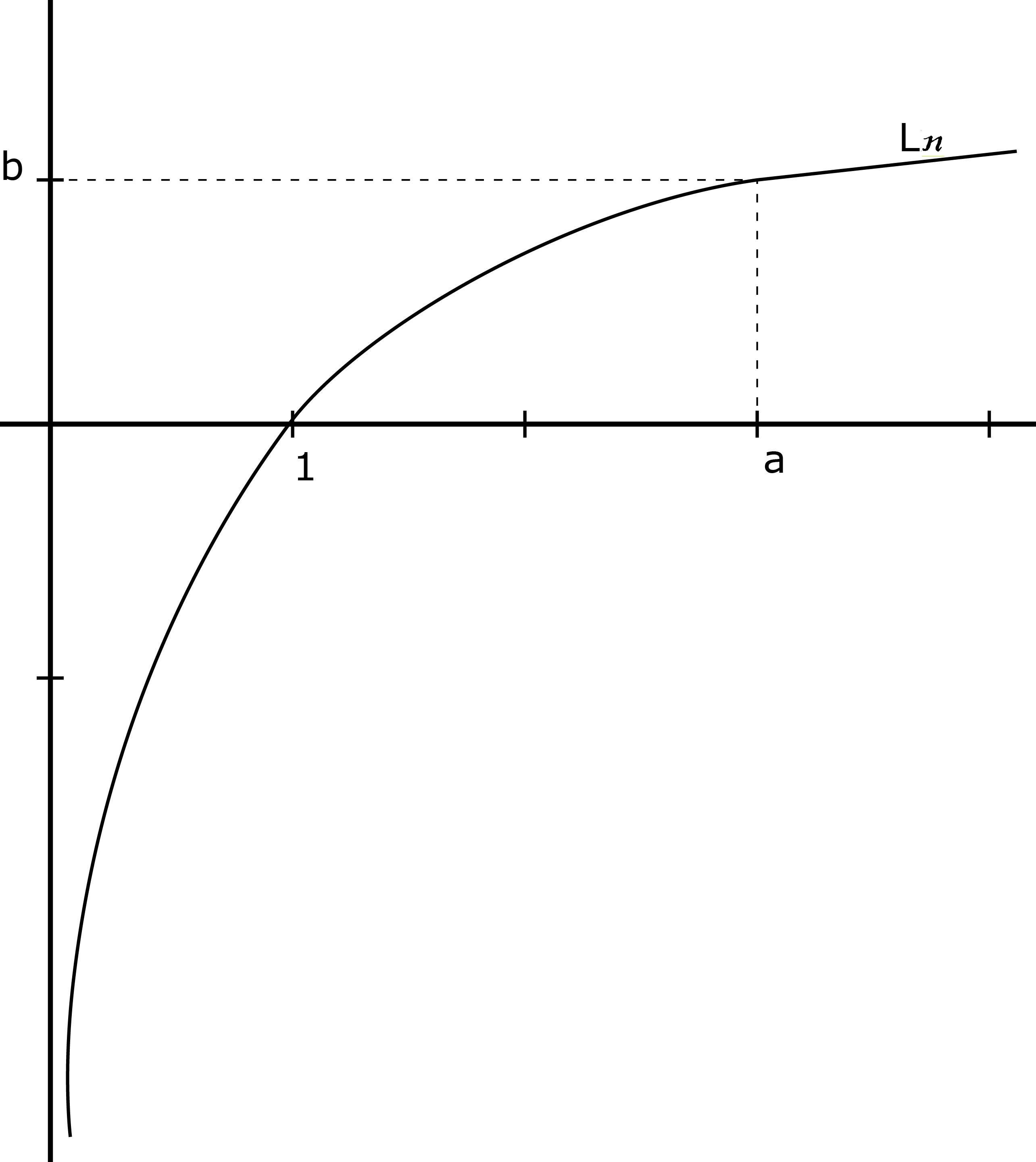
تسمى هذه الدالة"الدالة الأسية" و نرمز لها بالرمز
باستعمال الآلة الحاسبة نجد:
الدالة الأسية التي نرمز لها بالرمز
من أجل كل
- من أجل كل عدد صحيح نسبي لدينا:
- لدينا إذن من أجل كل عدد صحيح
- اصطلاحا نرمز: من أجل كل عدد حقيقي إلىبالرمز
- من أجل كل عدد حقيقي :
- من أجل كل من:
- من أجل كل منو من أجل كلمن:يعني
- من أجل كل من:و من أجل كلمن:
- من أجل كل عددين حقيقيين و:يكافئ
الدالة الأسية متزايدة تماما على
حل المعادلة :
لدينا:
حل المتراجحة
من أجل كل عددين حقيقيين
الإثبات : لدينا من جهة
و من جهة أخرى
إذن :
من أجل كل عددين حقيقيين
- منه
-
- لدينا من جهة: و من جهة أخرىمنه
الدالة الأسية معرفة على
- (تقبل دون برهان).
- نضع إذن لمافإن:
لأن
من أجل كل
نعتبر الدالة
نلاحظ أن
لدينا من جهة
ومن جهة أخرى : باستعمال مشتقة الدالة اللوغاريتمية مركبة نجد :
إذن:
من أجل كل
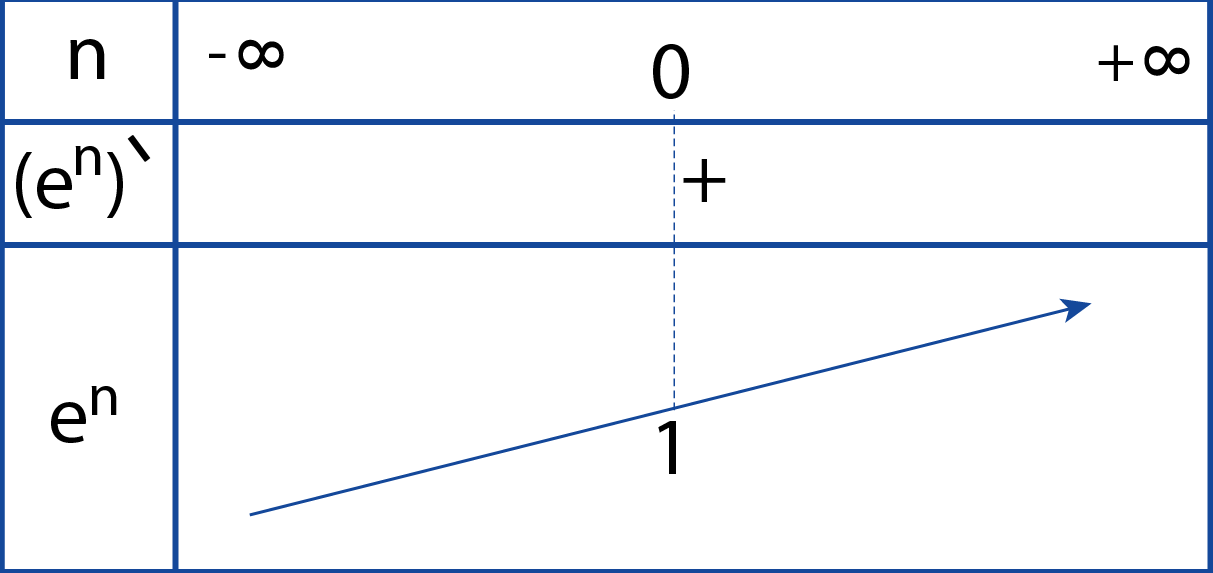
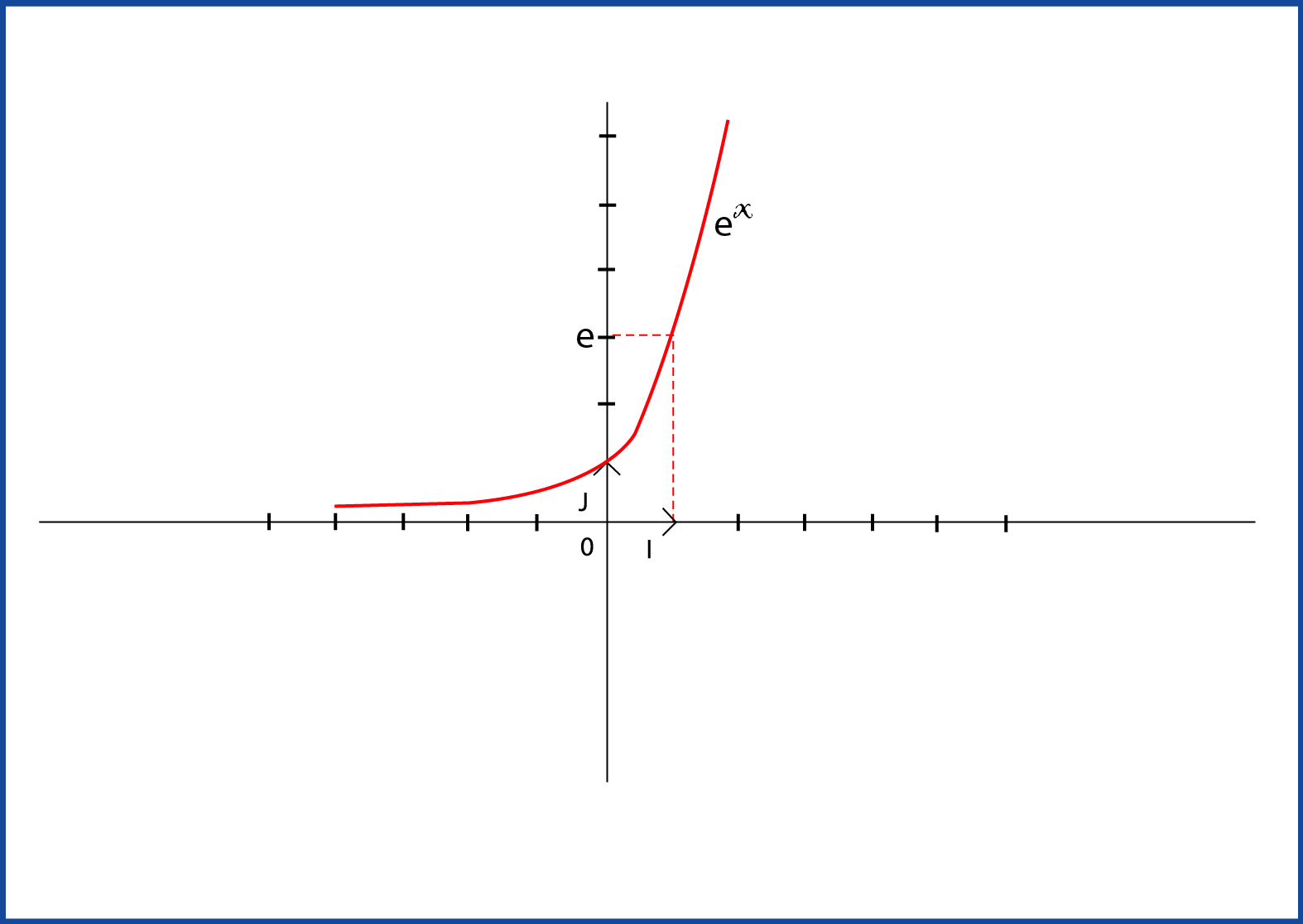
إذا كانت









