الإحتمالات المتساوية على مجموعة منتهية
بصفة عامة نرمز بـ:
نرمز بـ:
الحادثة
الحادثة الأولية هو حادثة يشمل إمكانية واحدة مثل:
نرفق بكل حادثة أولية
و
بهذا نكون قد عرّفنا احتمال على
احتمال الحادثة
إذا كان
إذا كان
نقول عن حوادث أولية أنها متساوية الإحتمال إذا كان
و هذا مهما كان
عدد الحالات الملائمة لتحقيق
نعتبر الحوادث:
و
احسب
توجد
توجد
لتكن
عندما نرفق بكل مخرج لتجربة عشوائية بعدد حقيقي تكون قد عرّفنا متغيّر عشوائي على
إذن المتغير العشوائي
معرف كما يلي:
ارفاق القيم :
نرمي حجر نرد متجانس مرقم
و نربح
قيم المتغير العشوائي هي:
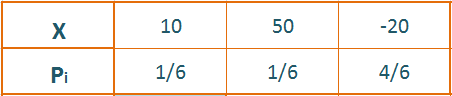
الأمل الرياضي للمتغير العشوائي
التباين للمتغير العشوائي
الانحراف المعياري للمتغير العشوائي
في المثال السابق (أعلاه) لدينا:
الاحتمال الرياضي لهذه اللعبة هي :
التباين هو :
الانحراف المعياري :
لتكن
صندوق يحوي
و يحوي أيضا
- ما احتمال الحصول على رقمين زوجين؟
نسمي
و
- واضح أن : و نريد حسابلدينا:
لكن
- و بالتالي:
نسمي تجزئة مجموعة أجزاء لهذه المجموعة ليست خالية كلها و منفصلة مثنى مثنى
(أي تقاطع كل جزأين خال) و اتحادهما المجموعة الكلية أي :
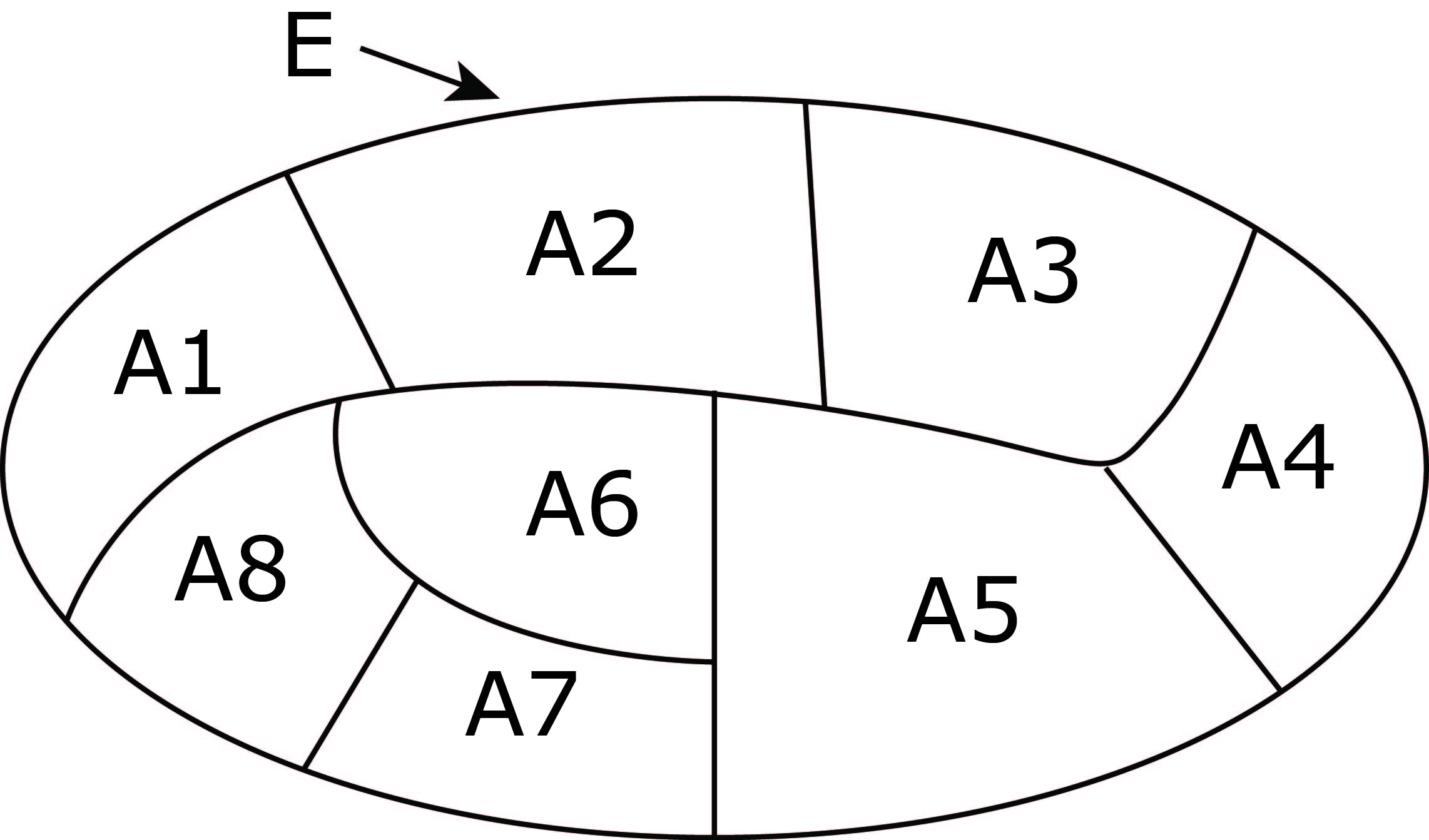
لتكن
- لدينا من أجل كل حادثة :
مع :
- لاحظ أن العائلة : تشكل تجزئة للحادثة .
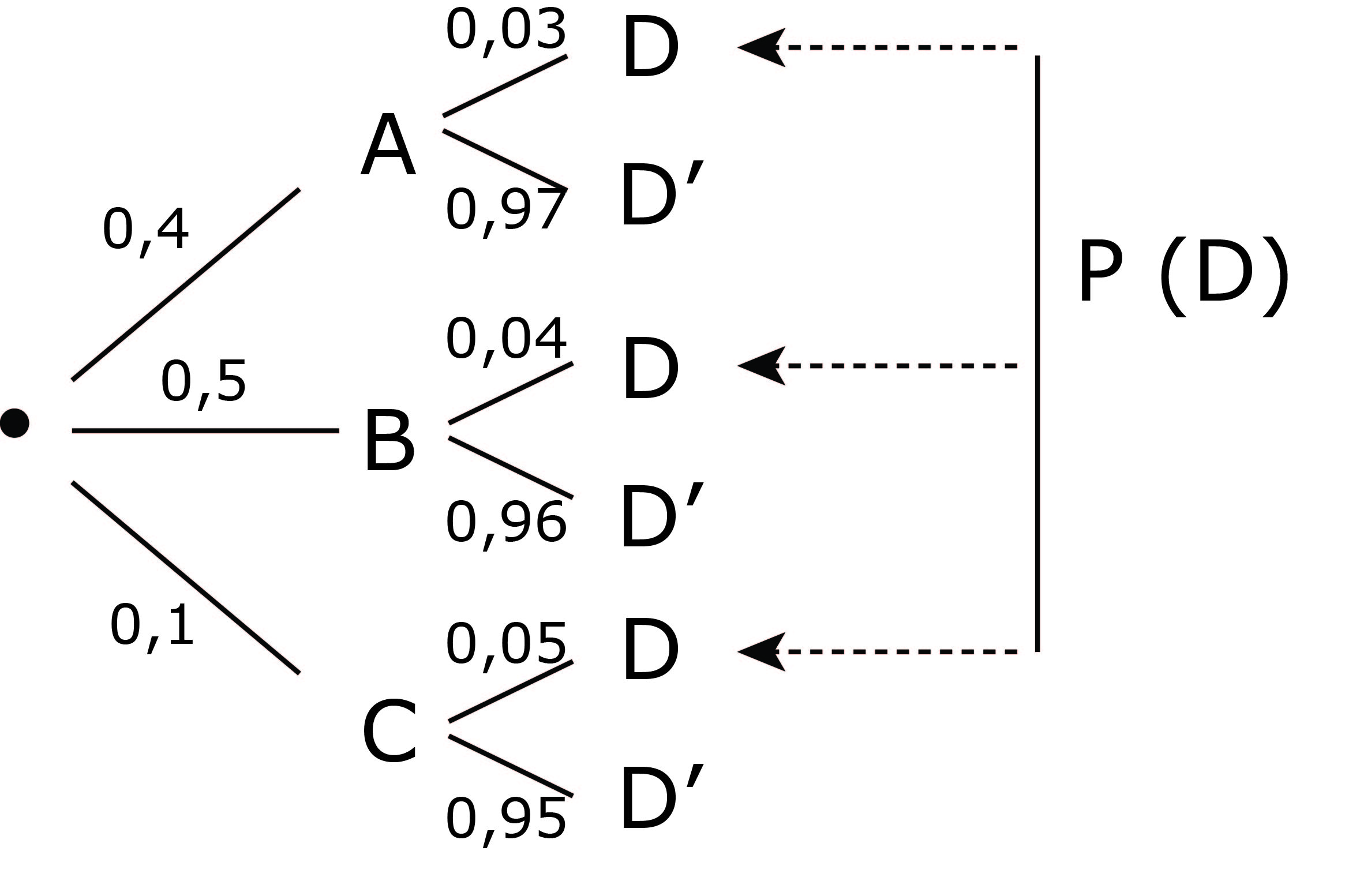
ثلاث آلات
- ما هو احتمال ان يكون البرغي فاسدًا؟
إذا علمت انه فاسد ما هو احتمال أنه أنتج من الآلة
نستعمل شجرة الاحتمالات
نسمي
احتمال هذا الحادث هو :
- إذن :
نقول عن حادثتين
- إذا كان :.
- إذا كان : فإن.
لتكن
قيم المتغير
- نقول أن ومستقلان عندما تكون الحادثتانو.
مستقلتان من اجل كل
- في حالة استقلال الحوادث يكون احتمال قائمة النتائج هو جداء إحتمالات كل النتائج (يحصل هذا عموما في التجارب العشوائية المكررة).
متغيران عشوائيان مرتبطان بتجربتين مستقلان.
نرمي
- ما هو احتمال الحادثة حيث "نحصل مرة واحدة على الأقل رقم فردي"
لو فكرنا في الاجابة المباشرة (الحصول على رقم فردي واحد فقط أو رقمين فرديين فقط أو ....أو كل الأرقام فردية).
فإن الحساب سيكون طويلا و معقدا نوعا ما، و عليه نفضل استعمال الخاصية التي تنص على ما يلي : " مجموع احتمالي حادثتين متعاكستين يساوي
- ومنه :
- إختبارات
- 5
- الأجوبة الصحيحة
- False
- الأجوبة الخاطئة
- False
- مجموع النقاط
- False
المراتب الخمس الأولى في Quiz
- sara bouras
- 108 نقطة
-

- abderahim op13
- 26 نقطة
-

- مسعودة أزرغاف
- 15 نقطة
-

- imadrass imadrass
- 3 نقطة
-

- ryma admin2
- 0 نقطة
-

- fouzia khelfane
- 0 نقطة
-

- Haddad Ouassini
- 0 نقطة
-

- ოპ ივ
- -3 نقطة
-









