الأشعة والهندسة التحليلية
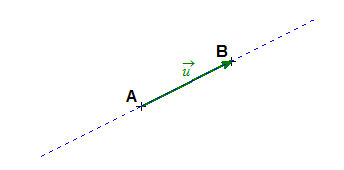
- إذا كانت ونقطتين من المستوي، الثنائيةتعيّن شعاعا
نكتب
- إذا كانت منطبقة علىفإن الثنائيةتعين الشعاع المعدوم
نكتب
- نسمي طول القطعة المستقيمة طويلة الشعاعونرمز إليها بالرمزونكتب:
- إذا كان شعاعا غير معدوم فإن منحى الشعاعهو منحى المستقيم
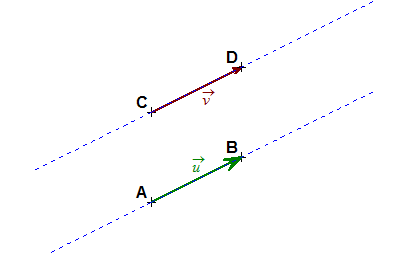
- إذا كان الشعاعين ولهما نفس المنحى و إذا كانممثلا للشعاعوممثلا للشعاعفإن :
الشعاع المعدوم ليس لم منحى
(
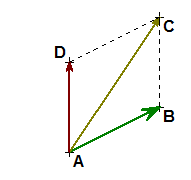
من أجل كل أربعة نقط
مجموع الشعاعين
إذا كان
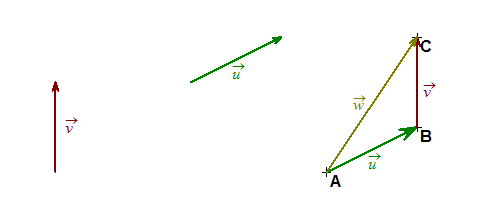
إذا كانت
إذا كانت
من أجل كل ثلاثة أشعة
- يوجد شعاع حيث
ونسمي الشعاع
إذا كانت
- تكافئ (منتصف القطعة
نسمي جداء الشعاع الغير معدوم
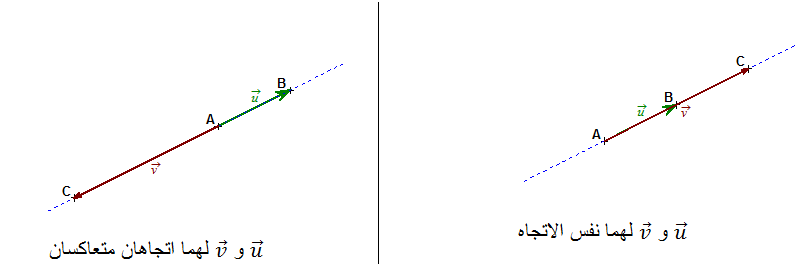
- ولهما نفس المنحى ونفس الاتجاه إذا كان
- ولهما نفس المنحى واتجاهان متعاكسان إذا كان

من أجل كل عددين حقيقيين
- تكافئأو
نقول أن الشعاعين
الشعاعين
الشعاع المعدوم مرتبط خطيا مع أي شعاع
يكون شعاعين غير معدومين مرتبطين خطيا إذا وفقط إذا كان لهما نفس المنحى
- يكون المستقيمان ومتوازيان إذا و فقط إذا كان الشعاعانومرتبطان خطيا
- تكون النقط على استقامة واحدة إذا و فقط إذا كان الشعاعانومرتبطان خطيا
نسمي النقطة
نسمي المحور
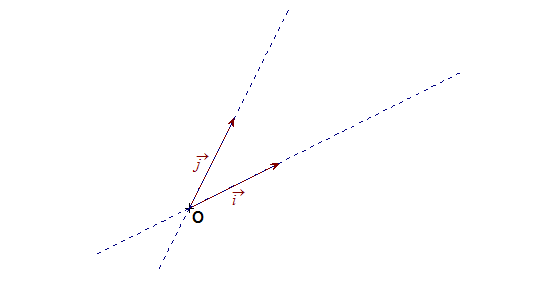
- إذا كان ومتعامدان فإن المعلممتعامد
- إذا كان ومتعامدان وفإن المعلممتعامد و متجانس
المستوي منسوب إلى المعلم
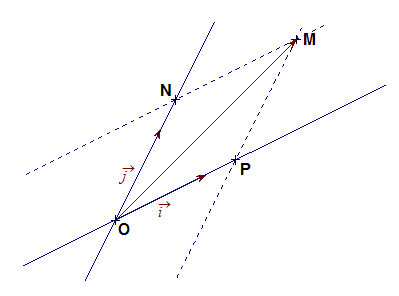
- من أجل كل نقطة من المستوي توجد ثنائية وحيدةمن الأعداد الحقيقية حيث :
نسمي الثنائية
- من أجل كل شعاع من المستوي توجد ثنائية وحيدةمن الأعداد الحقيقية حيث:
نسمي الثنائية
لتكن
الفواصل يقطع حامل محور التراتيب في النقطة
يقطع حامل محور الفواصل في النقطة
الشعاعين
الشعاعين
و بما أن
و منه توجد ثنائية وحيدة
▪ ليكن
نعلم أن توجد ثنائية وحيدة
نستبدل
في المستوي المنسوب إلى المعلم ، إذا كان
- إذا و فقط إذاو
-
بالنسبة للمعلم
نلاحظ أن :
معناه
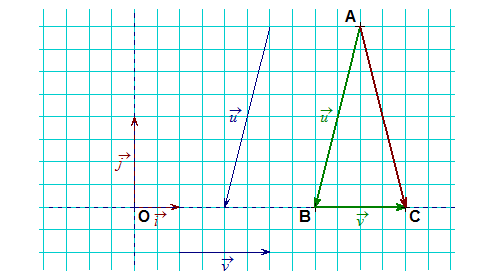
إذا كان المستوى منسوب إلى المعلم
- إحداثيا النقطة منتصف القطعةهما
لدينا
و لدينا
و منه
▪ نضع
فإن
و منه
في المستوي المنسوب إلى المعلم، إذا كان
(
و منه
- نفرض أن ويحققان
إما أحدهما معدوم (أو الاثنان معدومان) ففي هذه الحالة الشعاعين مرتبطين خطيا لأن الشعاع المعدوم مرتبط خطيا مع أي شعاع
إما الشعاعين غير معدومان ففي هذه الحالة من بين المركبات
نفرض مثلا أن
نضع
إذا كان المعلم منسوب إلى المعلم متعامد ومتجانس
نسمي شعاع توجيه المستقيم
إذا كان
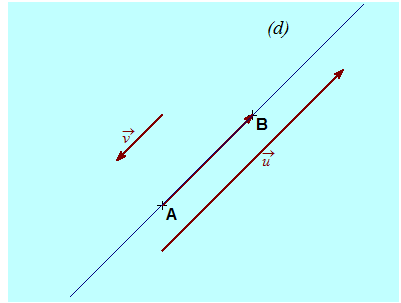
في المستوي منسوب إلى المعلم
نسمي معامل توجيه مستقيم المركبة الثانية لشعاع توجيه لهذا المستقيم مركبته الأولى هي 1
وهذا معناه
في المستوي منسوب إلى المعلم
▪ لكل مستقيم موازي لحامل محور التراتيب معادلة من الشكل
▪ مجموعة النقط
التراتيب
المستوي منسوب إلى المعلم
▪ ليكن
ولتكن
و منه
و منه للمستقيم
- نقطة من المجموعة المتكونة من النقطمن المستوي حيثمنهو بما أنفإنو منهمنهيوازي حامل محور التراتيب
لكل مستقيم
- مجموعة النقط من المستوي حيثعلما أنوعددان حقيقيان هي مستقيم غير
موازي لحامل محور التراتيب ذو شعاع توجيه
لتكن
نقطة من المستوي
و منه
و منه
و بما أن
و منه
نضع
▪ لتكن
و بما أن
و منه
مع
من المستوي حيث
إذا كانت
المستقيم
في المستوي المنسوب إلى معلم
المستقيمان
إذا
نعلم أن
نسمي جملة معادلتين خطيتين للمجهولين الحقيقيين
علما أن
و نسمي محدد الجملة
و الذي يساوي:
لتكن الجملة
إذا كان محدد الجملة
إذا كان محدد الجملة
- نعتبر الجملة ، محددها هو العدد الحقيقي
و يساوي
و بما أنه يختلف عن
من المعادلة الثانية نستخرج
و نجد
و منه الجملة
--------------------------------------------------------------
- نعتبر الجملة
، محددها هو العدد الحقيقي
و يساوي
و بما أنه يساوي
نستخرج نفس المجهول (مثلا
نلاحظ أن الجملة مستحيلة لأن
لا تقبل حلول
--------------------------------------------------------------
- نعتبر الجملة
، محددها هو العدد الحقيقي
و يساوي
و بما أنه يساوي 0 فالجملة
نستخرج نفس المجهول (مثلا
نلاحظ أن الجملة متكونة من نفس المعادلة ومنه الجملة تقبل عدد غير منتهي من الحلول و هي كل الثنائيات
- إختبارات
- 20
- الأجوبة الصحيحة
- False
- الأجوبة الخاطئة
- False
- مجموع النقاط
- False
المراتب الخمس الأولى في Quiz
- Bouaziz Sofiane
- 260 نقطة
-
- Ines RAHEB
- 220 نقطة
-

- Elhouda Lough Nour
- 215 نقطة
-

- wahab abdou
- 200 نقطة
-

- Hanouna Janine
- 200 نقطة
-
- Nessrine Meriem
- 200 نقطة
-

- habiba benabdallah
- 200 نقطة
-

- mar wa
- 200 نقطة
-

- اية عمران
- 200 نقطة
-

- Tryndamere Gnar
- 192 نقطة
-










