الدوال المستمرة و الغير مستمرة على مجال
- ادخال مفهوم الاستمرارية
- اعطاء جدول الدوال المستمرة
- اعطاء أمثلة مضادة
القول أن
القول أن
نلاحظ بيانيا أن المنحنى
منه الدالة
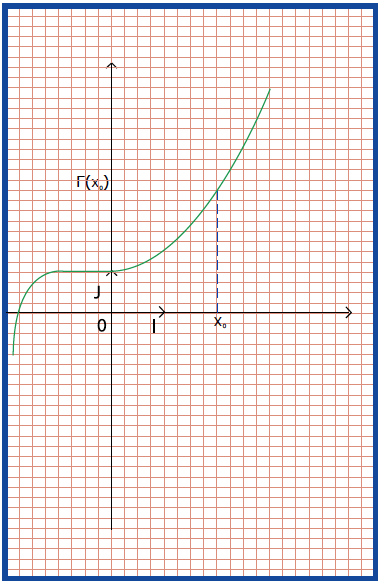
الدالة
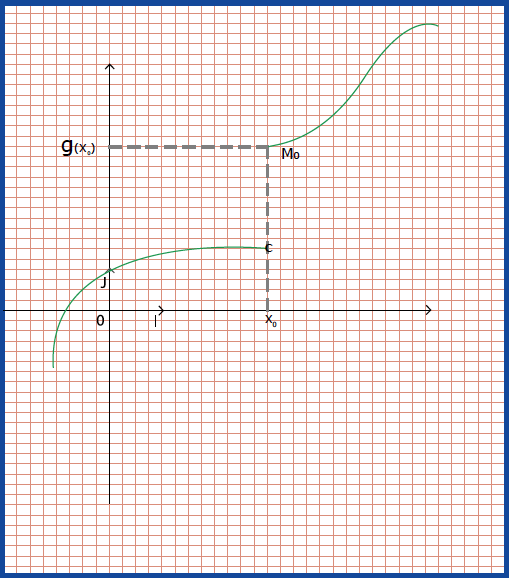
الدالة
هي دالة مستمرة عند
الدالة الجزء الصحيح لـ
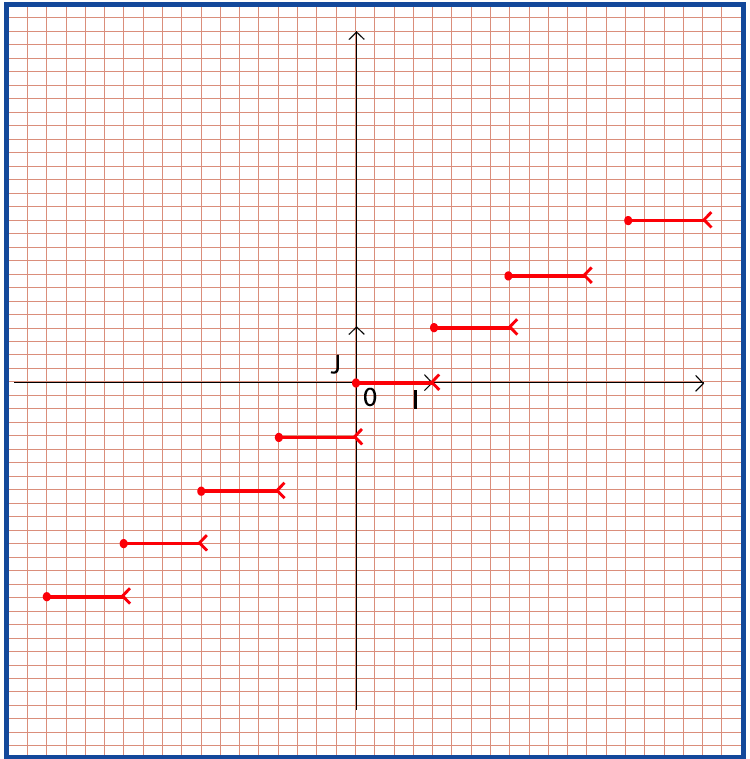
القول أن الدالة
الدالة
- الدوال كثير حدود مستمرة على
- الدالة مقلوب هي دالة مستمرة على
- الدالة جذر تربيعي هي دالة مستمرة على المجال
- الدالة القيمة المطلقة هي دالة مستمرة على
- الدوال المثلثية هي دوال مستمرة على
مجموع و جداء دالتين مستمرتين معرفتين على نفس مجال التعريف هما دالتان مستمرتان.
إذا كانت
- الدوال الناطقة هي دوال مستمرة على مجال تعريفهما لأنها حاصل قيمة دالتين مستمرتين
- الدوال جذر تربيعي لدوال موجبة و مستمرة هي دوال مستمرة
- الدوال الأسية و اللوغاريتمية هي دوال مستمرة
- الدالة المعرفة علىبـ :هي جداء الدالتين:والمستمرتان علىو منه الدالةمستمرة على
القول أن
القول أن









