الدالة الأسية تغيرات و النهايات
- دراسة الدالة الأسية
- اعطاء النهايات الشهيرة للدالة الأسية المفيدة في حالات عدم التعيين
- مشتق الدالة الأسية
الدالة الأسية متزايدة تماما على
لدينا من أجل كل
ومنه الدالة
من أجل كل ثنائية
الدالة
لدينا الخاصيتبن التاليتين:
- لإثبات الخاصية : نبرهن أولا على المتراجحة التالية : من أجل كلمن:. لذلك نضع:
الدالة
حسب نظرية
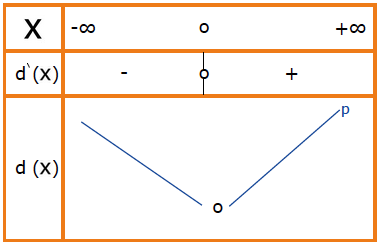
جدول تغيرات الدالة
إذن من أجل كل
منه
و بما أن
- لإثبات الخاصية : لدينا:
لدينا:
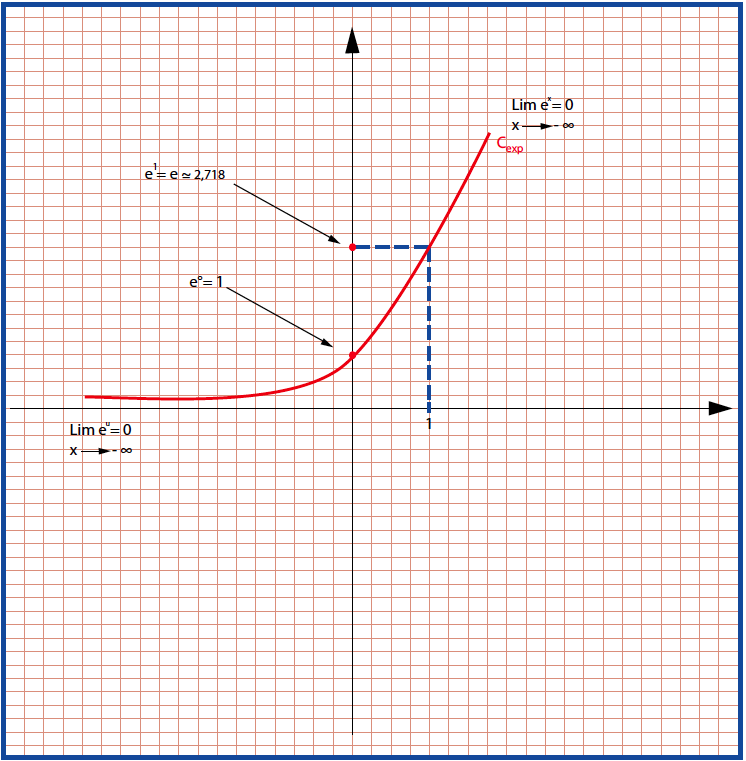
المماس للمنحنى
إذن محور الفواصل هو مقارب لـ
لتكن
الدالة
حالة خاصة : من أجل كل









