الدالة اللوغارتمية النيبيرية التغيرات و النهايلت
- دراسة الدالة اللوغاريتمية النيبيرية
- إعطاء النهايات الشهيرة للدالة اللوغاريتمية المفيدة في حالات عدم التعيين
- إعطاء مشتق تداول اللوغاريتيمة.
الدالة
الإثبات: ليكن
لدينا:
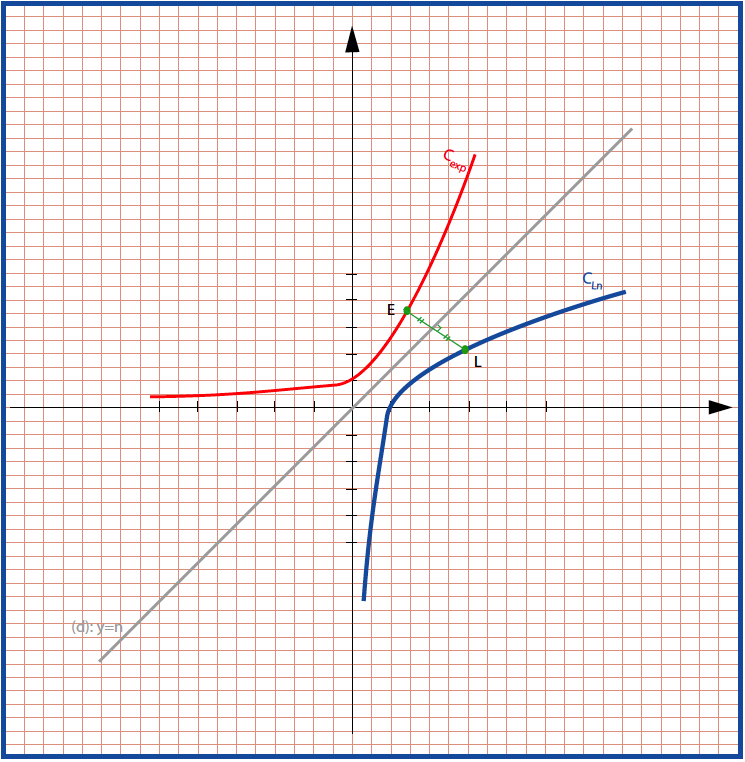
في معلم متعامد و متجانس للمستوى :التمثيلان البيانيين للدالتين
ليكن
نضع
لدينا:
أيضا النقطة
منه
لدينا الخواص التالية:
الخاصية
-ليكن
الخاصية
لدينا:
نضع
لما
نستعمل الدالة الأسية و اللوغاريتمية المتزايدتين على مجموعتين تعريفهما.









