الجداء السلمي الهندسة في الفضاء
- معرفة تعاريف الجداء السلمي في الفضاء
- فهم العبارة التحليلية للجداء السلمي
إذا كان
- الجداء السلمي للشعاعين وهو الجداء السلمي للشعاعينفي المستوي.إذن :
إذا كان:
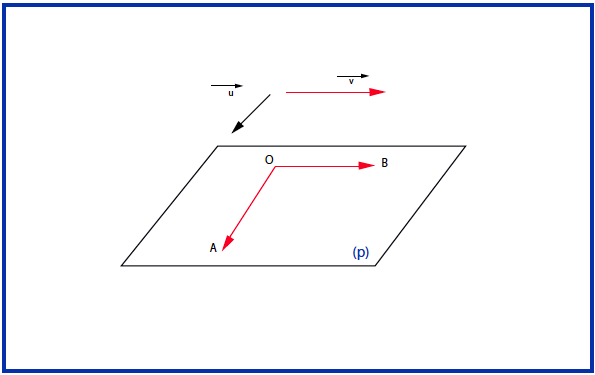
إذن
كما في المستوى شعاعان متعامدان إذا و فقط إذا كان جداءهما السلمي معدوم:
الشعاع المعدوم عمودي على كل الأشعة في الفضاء
طويلة الشعاع
لدينا
متعامدة مثنى مثنى و طويلها تساوي
مهما كانت الأشعة
إذن
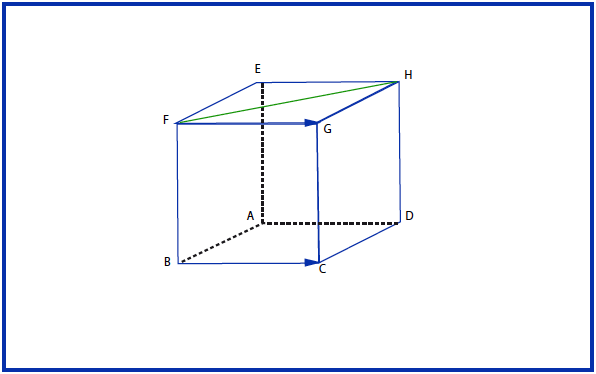
إذا كان في معلم متعامد و متجانس
و
في معلم متعامد و متجانس
لدينا:
- ;;;;و
- إذنعمودي على
- و
المثلث
المثلث
لإيجاد قيس الزاوية
إذن









