المعادلة الديكارتية لمستوى في الفضاء
- معرفة الشعاع الناظم لمستوي
- كتابة المعادلة الديكارتية لمستوي
نسمي شعاع ناظم لمستوي
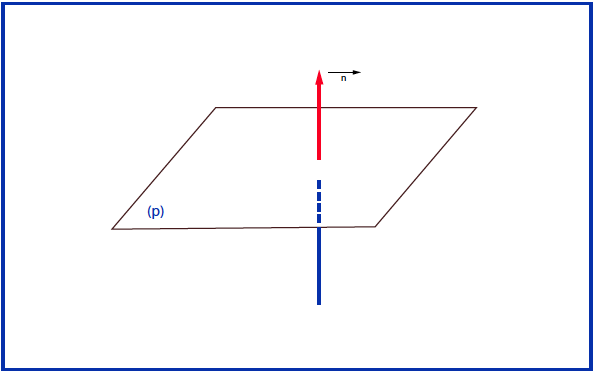
إذا كان
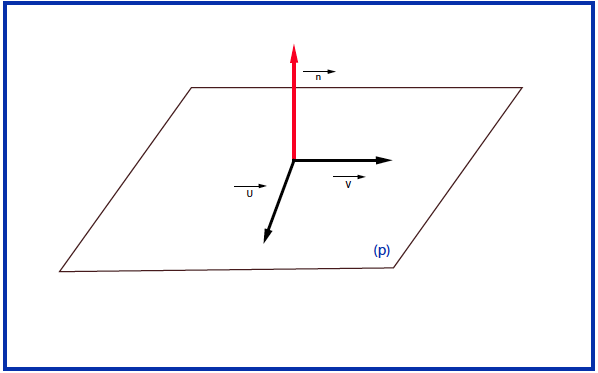
في معلم متعامد و متجانس كل مستو له معادلة من الشكل
و بالعكس :
في معلم متعامد ومتجانس لإيجاد معادلة ديكارتية لمستوي من الشكل
نتبع الطريقة التالية:
- نعرف الشعاع العمودي علىوفنتحصل على شعاع ناظمي للمستويو على المعاملاتللمعادلة المطلوبة
ليكن في معلم متعامد و متجانس النقط:
- تبيين أن معادلة المستوي هي :
لدينا $$\overrightarrow{AB}\Biggl(\begin{array}{ccc} -3\\ 1\\ 2 \end{array}\Biggr)$$ و $$\overrightarrow{AC}\Biggl(\begin{array}{ccc} -7\\ -2\\ 4 \end{array}\Biggr)$$ ليسا مرتبطان خطيا
إذن النقط $$B,A$$ و $$C$$ تعين مستو:
$$\vec {n}.\overrightarrow{AB}=0 \Leftrightarrow \vec{n}\Biggl(\begin{array}{ccc} a\\ b\\ c \end{array}\Biggr) \perp\overrightarrow{AB}\Biggl(\begin{array}{ccc} -3\\ 1\\ 2 \end{array}\Biggr)$$ منه $$-3a+b+2c=0$$
$$\vec {n}.\overrightarrow{AC}=0 \Leftrightarrow \vec{n}\Biggl(\begin{array}{ccc} a\\ b\\ c \end{array}\Biggr) \perp\overrightarrow{AC}\Biggl(\begin{array}{ccc} -7\\ -2\\ 4 \end{array}\Biggr)$$ منه $$-7a-2b+4c=0$$ نحل الجملة $$\begin{cases}-3a+b+2c=0\\-7a-2b+4c=0\end{cases}$$
التي تكافئ $$\begin{cases}-6a+2b+4c=0\\-7a-2b+4c=0\end{cases}$$
بالجمع نجد: $$-13a+8c=0$$
بالطرح نجد: $$a+4b=0$$
منه : $$\begin{cases}b=\frac{-a}{4}\\c=\frac{13a}{8}\end{cases}$$
إذا كان $$a=8$$ فإن $$b=-2$$ و $$c=13$$ إذن
$$\vec{n}\Biggl(\begin{array}{ccc} 8\\ -2\\ 13 \end{array}\Biggr)$$ شعاع ناظمي للمستوي $$(ABC)$$ و بالتالي معادلة $$(ABC)$$ هي : $$8x-2y+13z+d=0$$
$$A\epsilon (ABC)$$ إذن احداثيات $$A$$ وتحقق معادلة المستوي $$d=-15 \Leftrightarrow 8.4-2.2+13(-1)+d=0$$
معادلة المستوي $$(ABC)$$ هي :$$8x-2y+13z-15=0$$
في معلم متعامد و متجانس. نعتبر المستوي$$(P)$$ ذو المعادلة $$ax+by+cz+d=0$$ مع $$c,b,a$$ أعداد حقيقية ليست كلها معدومة
$$A$$ نقطة من الفضاء إحداثياتها
$$A(x_A,Y_A,3_A)$$. المسافة أو البعد بين النقطة$$A$$ و المستوي$$(P)$$ هو العدد الحقيقي الموجب:
$$d(A,P)=\frac {|ax_A+by_A+cz_A+d|}{\sqrt{a^2+b^2+c^2}}$$
في المعلم المتعامد و المتجانس :المسافة بين النقطة









