الأعداد المركبة: الشكل الجبري
- معرفة مجموعة الأعداد المركبة
- المستوي المركب و العمليات على الأعداد المركبة.
توجد مجموعة تسمى مجموعة الأعداد المركبة نرمز لها بالرمز
- تشمل المجموعةمجموعة الأعداد الحقيقية.
- مزودة بعمليتي الجمع و الضرب و نتبع نفس قواعد الحساب في المجموعة.
- يوجد عدد منحيث
- كل عدد منيكتب بطريقة وحيدة :حيثوعددان حقيقيان ,إذن,إذا كانو
فإن :
- , (وعددان حقيقيان ) تسمى الشكل الجبري للعدد المركب
- يسمى الجزء الحقيقي لـنرمز له بالرمز
- يسمى الجزء التخيلي لـنرمز له بالرمز
- إذا كان فإننقول أنحقيقي
- إذا كان فإننقول أنتخيلي بحت (أو تخيلي صرف)
- لكل عدد مركب نرفق النقطةتسمىصورةو نرمز لها بالرمز
- لكل نقطة من المستوي.يمكن أن نرفق العدد المركبتسمىلاحقة النقطة، يمكن أن نكتب
- لكل شعاع من المستوي يمكن أن نرفق العدد المركب.تسمىلاحقة الشعاعو نكتب.
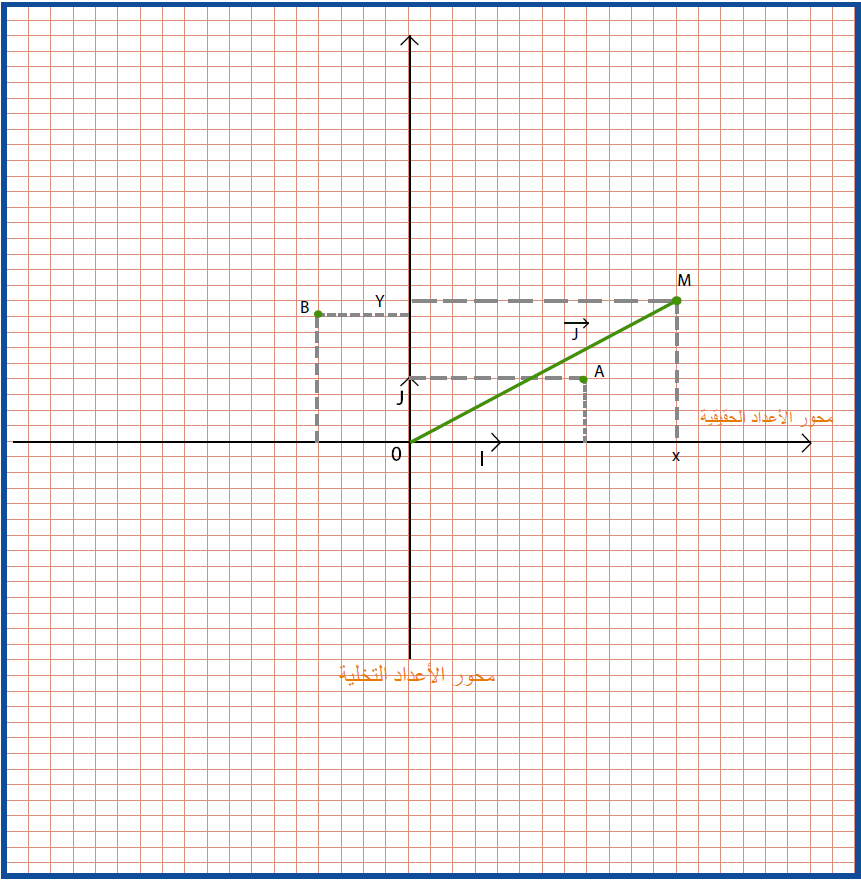
في المستوي المركب الصور:
إذا كان
إذا كان
العدد المركب
للحصول على مرافق عدد مركب
في المستوي المركب









