الطويلة ،العمدة، الشكل المثلثي
- حساب الاحداثيات القطبية، الطويلة و العمدة.
- كتابة الشكل المثلثي لعدد مركب.
الاحداثيات القطبية لنقطة
- إذا كانت هي احداثيات قطبية للنقطةفإن ثنائية من الشكلحيث :
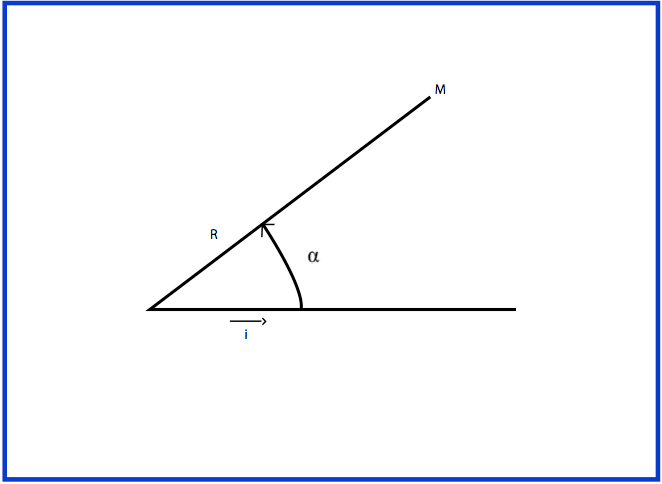
إذا كانت
لدينا
- نسمي طويلةو نرمز لها بالرمزأي:
- نسمي عمدة لـو نرمز لها بالرمزأي :
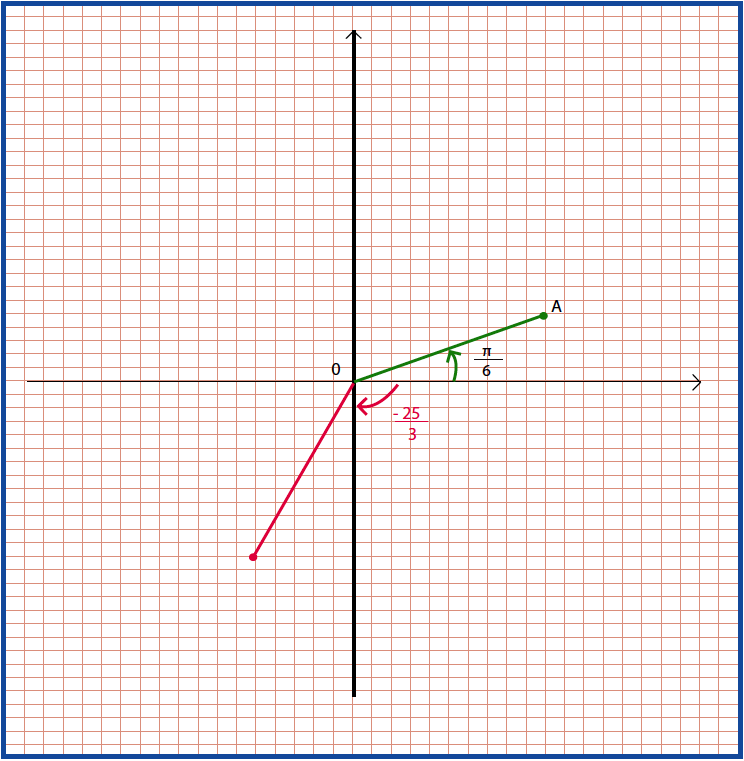
- إذا كان (وعددان حقيقيان ) فإن :
- من أجل كل عدد حقيقي غير معدوم : إذا كانفإنو إذا كان :فإن
- من أجل كل عدد تخيلي صرف مع, إذا كانفإنو إذا كانفإن
- إذا كان : وفإن :
- إذا كان معفإن:و
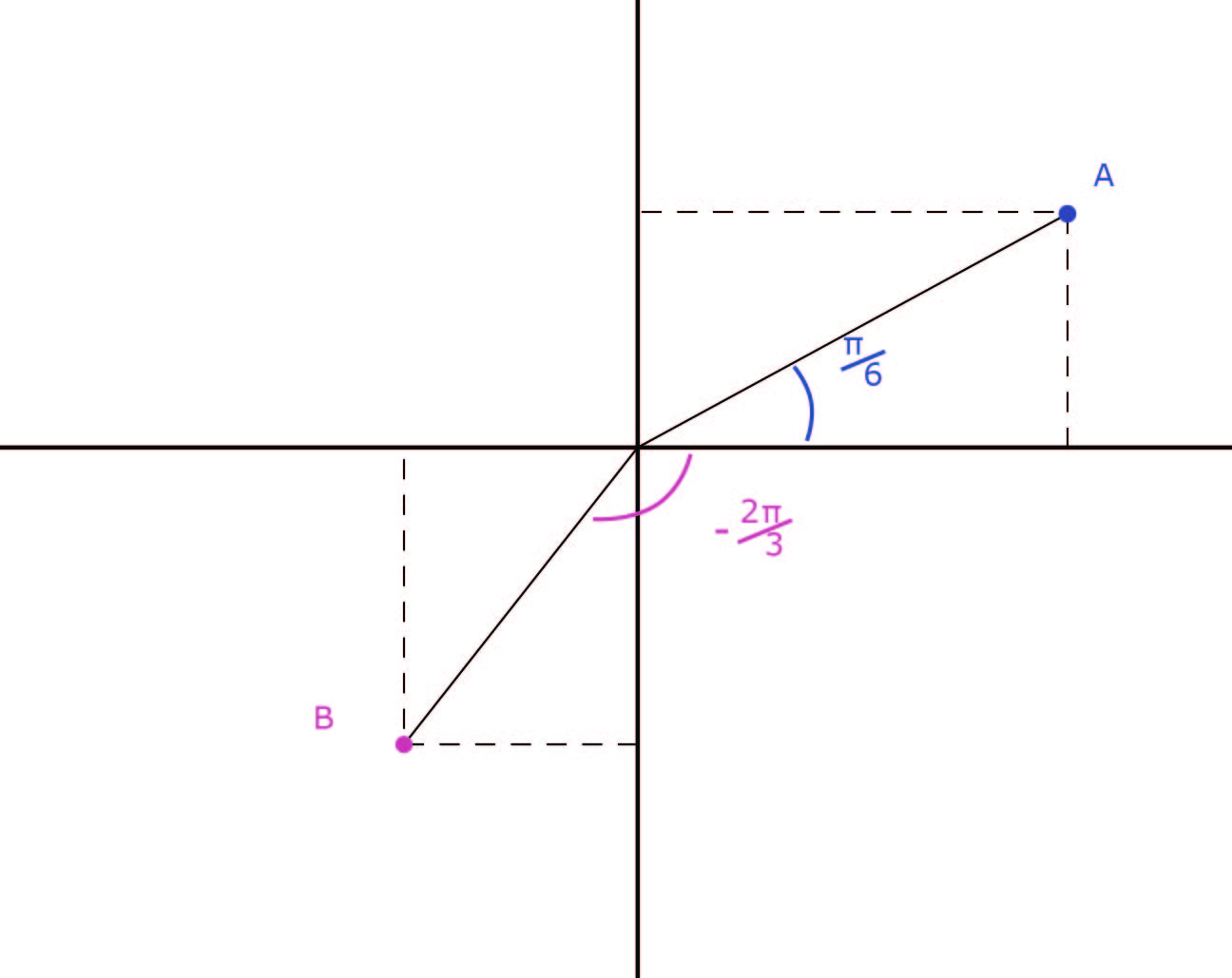
ليكن
إذا كان الشكل الجبري لـ
ليكن
إذن
الشكل المثلثي لـ
ليكن:
- هو معاكسيعني
- إذا كان عدد طبيعي فإن :
- إذا كان فإن :
- إذا كان فإن :
- لإثبات المساواة نستعمل البرهان بالتراجع
- بالنسبة للمقلوب لدينا :
إذا كان
منه
إذن
ومنه
في الأخير نبرهن على عبارة القسمة