الجداء السلمي و تطبيقاته
نسمي الجداء السلمي للشعاعين
- إذاو
- إذاأو
- الجداء السلمي لشعاعين عدد حقيقي و ليس شعاع
- إذا وفقط إذا كان (ومتعامدان).
الحالة الأولى :إذا كان
في هذه الحالة الحداء السلمي معدوم والشعاعين متعامدان (نقبل اصطلاحا أن اشعاع المعدوم عمودي على أي شعاع)
و منه الملاحظة صحيحة
الحالة الثانية : إذا كان
(
(
- و هذا من أجل كل شعاع
في المستوي الموجه توجيها مباشرا ، وحدة الطول هي السنتيمتر
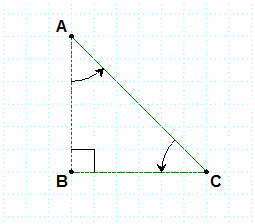
باستعمال مبرهنة بيتا قورس نحصل على $$AC=3\sqrt{2}$$ و منه
- $$\overrightarrow{AB}.\overrightarrow{AC}=AB.AC.\cos(\overrightarrow{AB};\overrightarrow{AC})$$ و منه $$\overrightarrow{AB}.\overrightarrow{AC}=3.3\sqrt{2}.\cos(\frac{\pi}{4})$$
$$\overrightarrow{AB}.\overrightarrow{AC}=9\sqrt{2}.\frac{\sqrt{2}}{2}=9$$
- $$\overrightarrow{AC}.\overrightarrow{CB}=AC.CB.cos(\overrightarrow{AB};\overrightarrow{AC})$$
$$(\overrightarrow{AB};\overrightarrow{AC})=(-\overrightarrow{CA};\overrightarrow{CB})=(\overrightarrow{CA};\overrightarrow{CB})+\pi+2k\pi=\frac{\pi}{4}+\pi+2k\pi$$ $$k،$$ عدد صحيح نسبي
منه $$\overrightarrow{AC}.\overrightarrow{CB}=3\sqrt{2}.3.\cos(\frac{\pi}{4}+\pi+2k\pi)$$ و منه $$\overrightarrow{AC}.\overrightarrow{CB}=3\sqrt{2}.3.[-\cos(\frac{\pi}{4}]$$
$$\overrightarrow{AC}.\overrightarrow{CB}=9\sqrt{2}.[-\frac{\sqrt{2}}{2}]=-9$$
$$A؛B$$ و $$C$$ ثلاثة نقط من المستوي حيث $$A \neq B$$
$$\overrightarrow{AB}.\overrightarrow{AC}=\overrightarrow{AB}.\overrightarrow{AH}$$ علما أن $$H$$ هو المسقط العمودي للنقطة $$C$$ على المستقيم $$(AB)$$ .
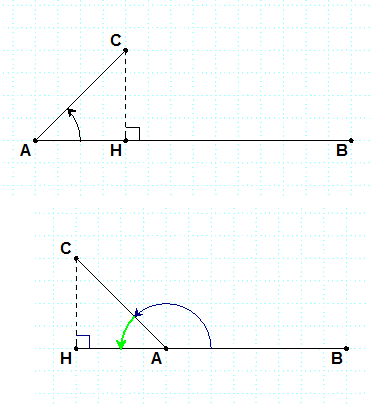
في الشكل الأول :
في الشكل الثاني :
و منه
في المثلث
و منه
من
إذا كانت
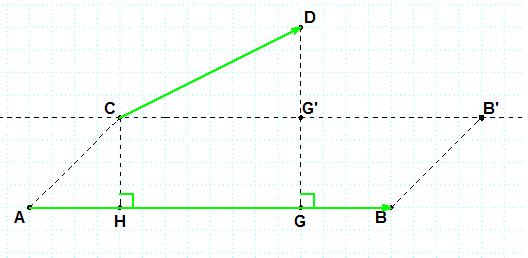
من أجل كل الأشعة
- و
و بما أن
و بما أن
------------------------------------------------------------------------
- إذا كان
و منه
- إذا كان
و منه
-------------------------------------------------------------------------------------------
علما أن
و منه من
المستوي الموجه توجيها مباشرا منسوب إلى المعلم المتعامد والمتجانس $$(0;\overrightarrow{i};\overrightarrow{j})$$
إذا كانت $$
\overrightarrow{u}\begin{pmatrix}
x\\
y
\end{pmatrix}_{(\overrightarrow{i};\overrightarrow{j})}
$$ و $$
\overrightarrow{v}\begin{pmatrix}
x^{'}\\
y^{'}
\end{pmatrix}_{(\overrightarrow{i};\overrightarrow{j})}
$$ فإن $$\overrightarrow{u}.\overrightarrow{v}=(x.x^{'}+y.y^{'})$$
نعلم أن $$(\overrightarrow{i} \perp \overrightarrow{j})$$ منه $$(\overrightarrow{i}.\overrightarrow{j}=0)$$ و $$[\|\overrightarrow{i}\|=\|\overrightarrow{j}\|=1]$$
$$\overrightarrow{u}=x\overrightarrow{i}+y\overrightarrow{j}$$ و $$\overrightarrow{v}=x^{'}\overrightarrow{i}+y{'}\overrightarrow{j}$$ و منه $$\overrightarrow{u}.\overrightarrow{v}=(x\overrightarrow{i}+y\overrightarrow{j})(x^{'}\overrightarrow{i}+y{'}\overrightarrow{j})$$
$$\overrightarrow{u}.\overrightarrow{v}=(x.x^{'}.(\overrightarrow{i}^{2})+xy^{'}(\overrightarrow{i}.\overrightarrow{j})+yx^{'}(\overrightarrow{i}.\overrightarrow{j})+yy^{'}.\overrightarrow{j}^{2})$$ و منه
$$\overrightarrow{u}.\overrightarrow{v}=(x.x^{'}.(\|\overrightarrow{i}\|^{2})+xy^{'}(\overrightarrow{j}.\overrightarrow{i})+yx^{'}(\overrightarrow{j}.\overrightarrow{i})+yy{'}.\|\overrightarrow{j}\|^{2})$$ و منه $$\overrightarrow{u}.\overrightarrow{v}=(x.x^{'}+y.y^{'})$$ .
- إذا كانت
(
--------------------------------------------------
- إذا كانت
فإن
$$\overrightarrow{u}.\overrightarrow{u}=x.x+y.y=x^{2}+y^{2}$$ و$$\overrightarrow{u}.\overrightarrow{u}=\|\overrightarrow{u}\|^{2}$$ و منه $$x^{2}+y^{2}=\|\overrightarrow{u}\|^{2}$$ و منه
$$\|\overrightarrow{u}\|=\sqrt{x^{2}+y^{2}}$$
- إذا كانت
$$
\overrightarrow{u}\begin{pmatrix}
x\\
y
\end{pmatrix}_{(\overrightarrow{i};\overrightarrow{j})}
$$ و $$
\overrightarrow{v}\begin{pmatrix}
x^{'}\\
y^{'}
\end{pmatrix}_{(\overrightarrow{i};\overrightarrow{j})}
$$
فإن: $$\cos(\overrightarrow{u};\overrightarrow{v})=\frac{x.x^{'}+y.y^{'}}{\sqrt{x^{2}+y^{2}}}.\sqrt{x^{'2}+y^{'2}}$$
-----------------------------------------------------------------------
- المسافة بين النقطتين $$A(x_A؛y_A)$$ و $$B(x_B؛y_B)$$ هي $$AB=\sqrt{(x_B-x_A)^2 + (y_B-y_A)^2}$$
نقول عن الشعاع الغير معدوم
أنه شعاع ناظمي للمستقيم
المستوي منسوب إلى المعلم المتعامد و المتجانس
و ليكن
للمستقيم ذو الشعاع النظمي
$$
\overrightarrow{n}\begin{pmatrix}
a\\
b
\end{pmatrix}
$$
معادلة من الشكل$$(ax+by+c=0)$$ حيث $$(a؛b) \neq (0؛0)$$
و العكس صحيح
كل معادلة من الشكل $$(ax+by+c=0)$$ مع $$(a؛b) \neq (0؛0)$$ هي معادلة مستقيم ذو الشعاع
$$
\overrightarrow{n}\begin{pmatrix}
a\\
b
\end{pmatrix}
$$ شعاع ناظمي.
نعلم أن $$(ax+by+c=0)$$ مع $$(a؛b) \neq (0 ؛0)$$ هي معادلة مستقيم ذو الشعاع التوجيه $$
\overrightarrow{u}\begin{pmatrix}
-b \\
a
\end{pmatrix}
$$
و بما أن $$
\overrightarrow{n}\begin{pmatrix}
a\\
b
\end{pmatrix}
$$ عمودي على $$
\overrightarrow{u}\begin{pmatrix}
-b\\
a
\end{pmatrix}
$$ فإن $$(ax+by+c=0)$$ مع $$(a؛b) \neq (0؛0)$$ هي معادلة مستقيم ذو الشعاع الناظمي $$
\overrightarrow{n}\begin{pmatrix}
a\\
b
\end{pmatrix}
$$ .
في المستوي منسوب إلى المعلم المتعامد و المتجانس
و بما أن
معادلة الدائرة التي مركزها
في المستوي منسوب إلى المعلم المتعامد و المتجانس
نعلم أن من أجل كل نقطة
و تكافئ
معادلة الدائرة التي قطرها
معادلة دائرة علم قطرها أو علم مركزها و نصف قطرها هي من الشكل
و العكس خاطئ ، ليست كل المعادلة من الشكل
المستوي منسوب إلى المعلم المتعامد و المتجانس
نسمي المسافة بين النقطة
نرمز إلى هذه المسافة بالرمز:
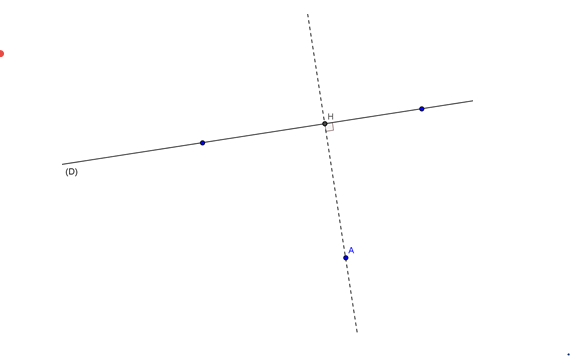
المستوي منسوب إلى المعلم المتعامد و المتجانس
إذا كان
ليكن
الشعاع ناظمي ل
لتكن
و بما أن
من
- إذا كانت النقطة منتصف القطعةفإن من أجل كل نقطةمن المستوي:
و منه
- إذا كان مثلث حيثووفإن:
- إذا كان مثلث حيثووفإن مساحة المثلثهيحيث :
- إذا كان مثلث حيثووفإن :
المستوي منسوب إلى المعلم المتعامد و المتجانس
نعتبر النقطتين
منه
نعلم أن إذا كانت
و منه
من
بالجمع
نضع
منه
بالطرح
بالجمع
بالطرح:
- إختبارات
- 20
- الأجوبة الصحيحة
- False
- الأجوبة الخاطئة
- False
- مجموع النقاط
- False
المراتب الخمس الأولى في Quiz
- mani gando
- 125 نقطة
-

- Merouane Kanoune
- 120 نقطة
-

- lina lili
- 119 نقطة
-

- yousra abdlmoumenaoui
- 115 نقطة
-

- mina boube
- 103 نقطة
-
- ha nane
- 92 نقطة
-

- oussama gsm
- 60 نقطة
-

- ibtihel ibtihel
- 57 نقطة
-

- Deadly Pride
- 48 نقطة
-

- Imene Imene
- 40 نقطة
-









