النهايات و المتتاليات
نقول أن العدد الحقيقي
- إذا كانت متقاربة فإن نهايتها وحيدة.
- إذا كانت متتالية غير متقاربة فهي متباعدة (نهايتها غير منتهية أو غير موجودة)
المتتاليات المعرفة بـ:
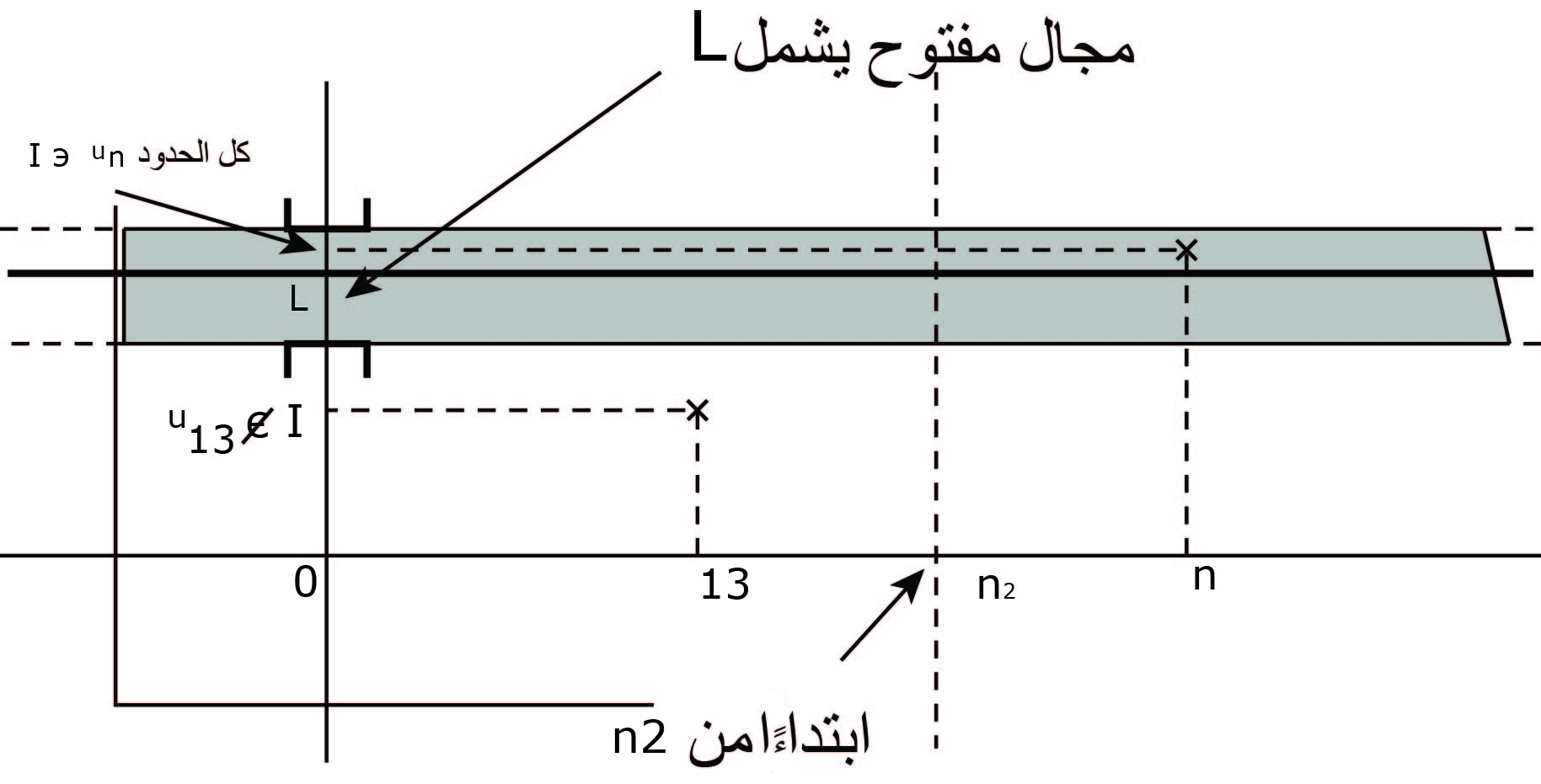
نقول أن متتالية
ويعني ذلك أن حدود المتتالية
الكتابة
المتتاليات
متتاليات لها النهاية
دراسة تقارب متتالية هندسية كيفية ذات الحد العام
- إذا كان فإن
- إذا كان أوفإن المتتاليةثابتة
- إذا كان فإن
- إذا كان فإنغير موجودة
- لتكن
بما أن
إذن المتتالية
- لتكن
بما أن
إذا كانت
و عليه فالمتتالية
إذاكانت
بوضع
بما أن
القواعد المتعلقة بنهايات الدوال عند
أما بالنسبة إلى نهاية المتتالية باستعمال الحصر لدينا المبرهنات التالية :
إذا كان ابتداءا من عدد طبيعي
و إذا كانت
فإن
- إذا كان من أجل كل لديناوفإن
- إذا كان من أجل كل لديناوفإن
- القول أن المتتالية محدودة من الأعلى يعني أنه يوجد عدد حقيقيبحيث أنه من أجل كل عدد طبيعيلدينا :
يسمى
- القول أن المتتالية محدودة من الأسفل يعني أنه يوجد عدد حقيقيبحيث أنه من أجل كل عدد طبيعيلدينا :
يسمى
- إذا كانت محدودة من الأعلى و من الأسفلل نقول أنها محدودة
- إذا كانت متتالية محدودة من الأعلى بالعددفإن كل الأعداد الحقيقية الأكبر منهي أيضا عناصر حادة لـ
نعرّف بنفس الكيفية العناصر الحادة من الأسفل.
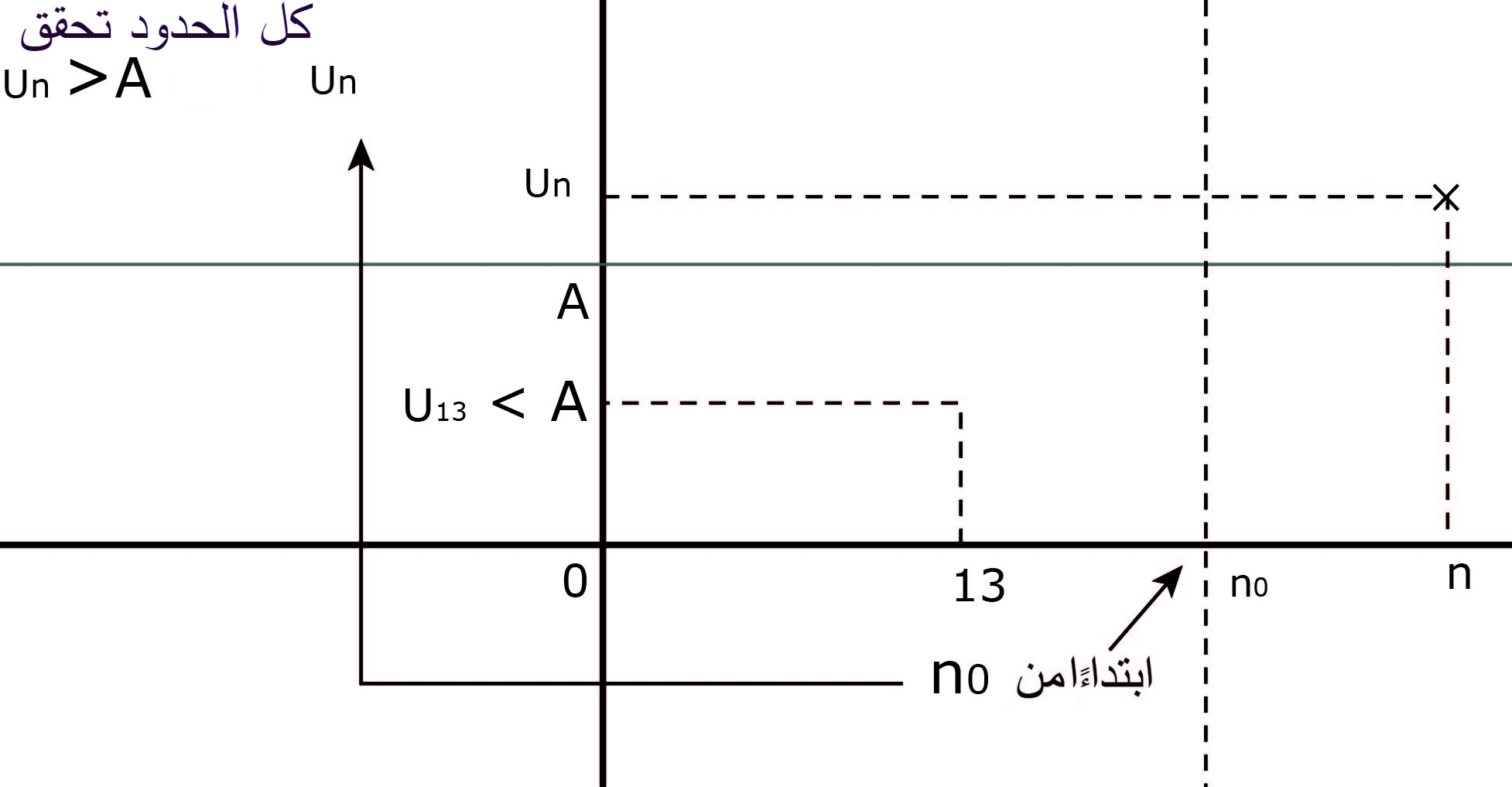
- نفي القضية "المتتالية غير محدودة من الأعلى " يعني أنه من أجل كل عدد حقيقيكبير بالقدر الكافي نستطيع أن نجد حدبحيث
- المتتالية المعرفة بـ :محدودة لأنه من أجل كل عدد طبيعي
لدينا:
- المتتالية محدودة لأنه من أجل كل عدد طبيعي
لدينا:
- المتتالية محدودة من الأعلى لأنه من أجل كل عدد طبيعي
لدينا
- كل متتالية متزايدة و محدودة من الأعلى فهي متقاربة.
- كل متتالية متناقصة و محدودة من الأسفل فهي متقاربة
- عين اتجاه تغير ثم استنتج أنمتقاربة
لدينا (
المتتالية
- معرفة و استعمال مفهوم متتاليتان متجاورتان.
القول أن المتتاليتين
لتكن
المتتالية
المتتالية
إذن
نستنتج أن المتتاليتان
إذا كانت المتتاليتان
في المثال السابق لدينا:
بما أن
و
إذن المتتاليتان









