الإشتقاقية 2
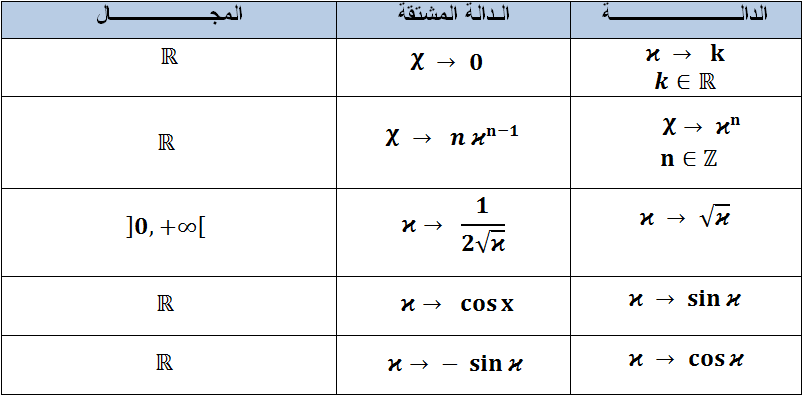
- معرفة مشتقات الدوال المرجعية
- معرفة العمليات على الدوال المشتقة
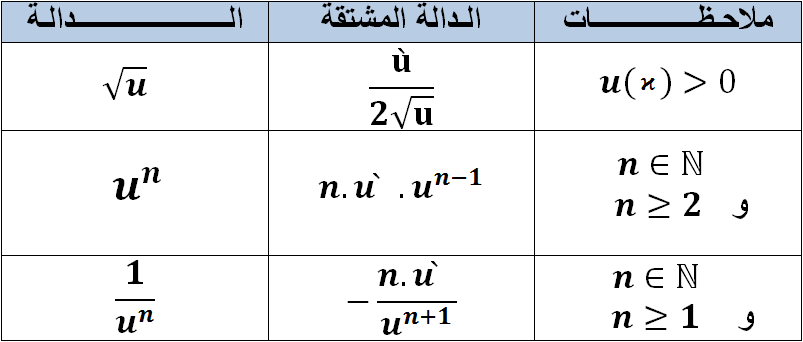
فيما يخص
إذاكانت
إذا كانت الدالة
- .
- .
- .
- .
- اعطاء تغيرات دالة انطلاقا من إشارة مشتق دالة
- العلاقة بين المشتق و القيم الحدية
- دراسة المشتق:هل دائما ضروري؟
لتكن
- إذا كانت الدالة المشتقة معدومة علىفإن الدالةثابتة على
- إذا كانت الدالة المشتقة موجبة تماما على(أو يمكن أن تنعدم من أجل قيم منعزلة) فإن الدالةمتزايدة تماما
- إذا كانت الدالة المشتقة سالبة تماما على(أو يمكن أن تنعدم من أجل قيم منعزلة) فإن الدالةمتناقصة تماما.
لتكن الدالة
و
على المجال
و منه الدالة
على المجال
لتكن
- و تقبل قيمة حدية محلية عندإذن
- إذا انعدمت الدالة المشتقة عندمغيرة إشارتها فإنتقبل قيمة حدية محلية عند
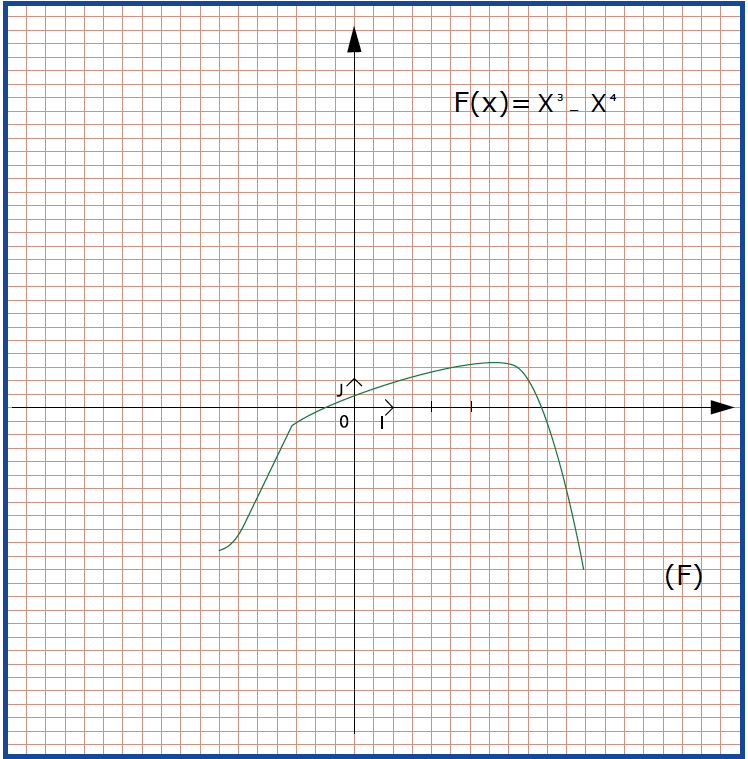
في المثال السابق:
لكن
صغيرة اشارتها إذن
إذا كانت
إذا كانت
إذا كانت الدالتان لهما نفس اتجاه التغير فإن
إذا كانت الدالتان ليس لهما نفس اتجاه التغير
- متزايدة علىلأنها مجموع دالتان متزايدتان علىلأنها مجموع دالتان متزايدتان على
- معرفة علىو هي مجموع دالتان متناقصتان علىإذنمتناقصة على
الدالة المركبة من الدالتين
و المعرفة على
الدالة
الدالة
إذا قبلت الدالة
لتكن
نلاحظ أن:
ومنه :
إذن:
باستعمال اشتقاق دالة مركبة نتحصل على النتائج التالية: