المعادلة الديكارتية لمستوى في الفضاء
- معرفة الشعاع الناظم لمستوي
- كتابة المعادلة الديكارتية لمستوي
نسمي شعاع ناظم لمستوي
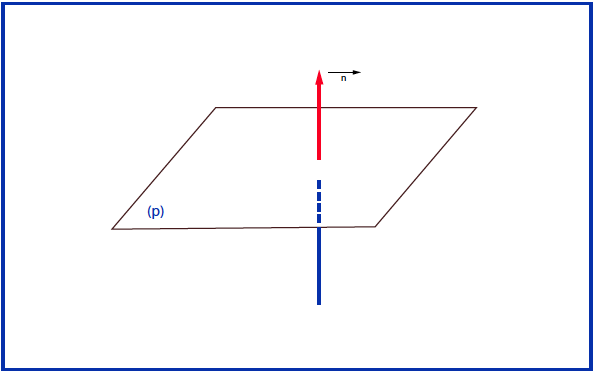
إذا كان
في معلم متعامد و متجانس كل مستو له معادلة من الشكل $$ax+by+cz+d=0$$ مع $$(a,b,c)\neq(0,0,0)$$و الشعاع $$\vec{n}\Biggl(\begin{array}{ccc} a\\ b\\ c \end{array}\Biggr)$$ ناظمي للمستوي $$P$$
و بالعكس : $$d,c,b,a$$ أعداد حقيقية حيث $$(a,b,c)\neq(0,0,0)$$ مجموعة النقط $$M(x,y,z)$$ حيث $$ax+by+cz+d=0$$ هي مستوي له شعاع ناظمي هو : $$\vec{n}\Biggl(\begin{array}{ccc} a\\ b\\ c \end{array}\Biggr)$$
في معلم متعامد ومتجانس لإيجاد معادلة ديكارتية لمستوي من الشكل
نتبع الطريقة التالية:
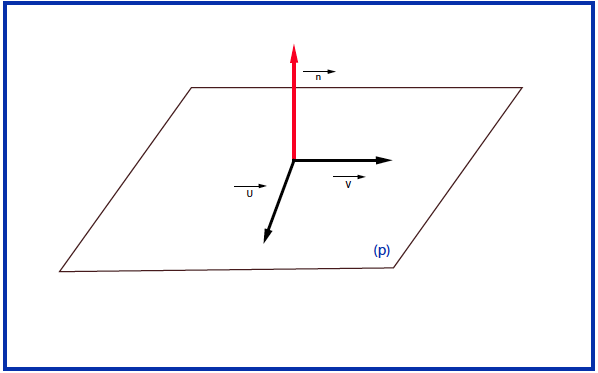
- نعرف الشعاع العمودي علىوفنتحصل على شعاع ناظمي للمستويو على المعاملاتللمعادلة المطلوبة
ليكن في معلم متعامد و متجانس النقط:
- تبيين أن معادلة المستوي هي :
لدينا
إذن النقط
التي تكافئ
بالجمع نجد:
بالطرح نجد:
منه :
إذا كان
معادلة المستوي
في معلم متعامد و متجانس. نعتبر المستوي
في المعلم المتعامد و المتجانس :المسافة بين النقطة









