تلخيص الدوال العددية
نسمي اللوغريتم النيبيري للعدد الحقيقي الموجب تماما
الدال اللوغاريتمية النيبيرية هي الدالة
- من أجل كل عدد حقيقي منلدينا:إذا كانوإذا كان.
- من أجلومن أجل
- من أجل كل عددين حقيقيين وموجبين تماما لدينا:
- من أجل كل عددين حقيقيين وموجبين تماما لدينا:
- من أجل كل عدد حقيقي موجب تماما و كل عدد ناطقلدينا:
- من أجل كل عدد حقيقي موجب تماما لدينا:
لدينا:
إذا وضعنا
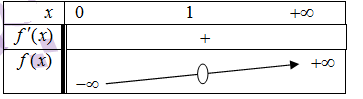
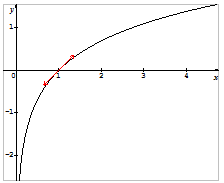
- من أجل كل عدد طبيعيو كذلكوكثير حدود.
- من أجل كل عدد طبيعيو كذلكحيثكثير حدود.
-
إذا كانت









