تلخيص الأعداد المركبة
نسمي عددا مركبا كل عدد
- العدد الحقیقي یسمى بالجزء الحقیقي للعددو نكتب:
- العدد الحقیقيیسمى بالجزء التخیلي للعددو نكتب:
- إذا كان نقول أن العددحقیقي.
- إذا كان نقول أن العددتخیلي صرف.
- الكتابة تسمى الشكل الجبري للعدد
- معناه أنوحیث
في المستوي المنسوب إلى معلم متعامد و متجانس
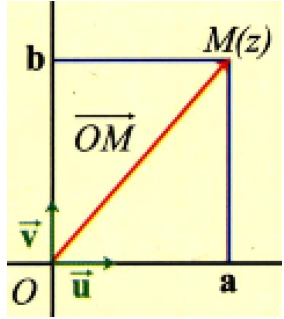
لیكن
إذا كان
مرافق العدد المركب
أكتب على الشكل الجبري العدد المركب
- ;
- ;
- ;
- , حیثعدد طبیعي غیر معدوم.
- إذا كان فإن:;
طویلة عدد مركب
- أحسب طویلة العدد المركب :
من أجل كل عددین مركبین
- مع
في المستوي المركب المنسوب إلى معلم متعامد و متجانس
نسمي عمدة العدد
إذا كان
یكون العدد المركب
- حقیقیا إذا و فقط إذا كان
- تخیلیا صرفا إذا و فقط إذا كان
- حقیقیا موجبا تماما إذا و فقط إذا كان
- حقیقیا سالبا تماما إذا و فقط إذا كان
في المستوي المركب المنسوب إلى معلم متعامد و متجانس
لاحقة الشعاع
المسافة بین نقطتین
تكون النقط
تكون النقط
لاحقة النقطة
- یكون المثلث متساوي الساقین رأسهإذا و فقط إذا كان
- یكون المثلث قائما فيإذا و فقط إذا كان
- یكون المثلث قائما فيو متساوي الساقین إذا و فقط إذا كانو
- یكون المثلث متقایس الأضلاع إذا وفقط إذا كان:وأو
- یكون الرباعي متوازي أضلاع إذا و فقط إذا كان:
- یكون الرباعي مستطیلا إذا و فقط إذا كان:و
- یكون الرباعي معینا إذا و فقط إذا كان:و
- یكون الرباعي مربعا إذا و فقط إذا كان:وو
- یكون الرباعي شبه منحرف إذا و فقط إذا كان:و
في المستوي المنسوب إلى المعلم المتعامد المتجانس المباشر، نعتبر التحویل النقطي
یمكننا تلخیص طبیعة التحویل
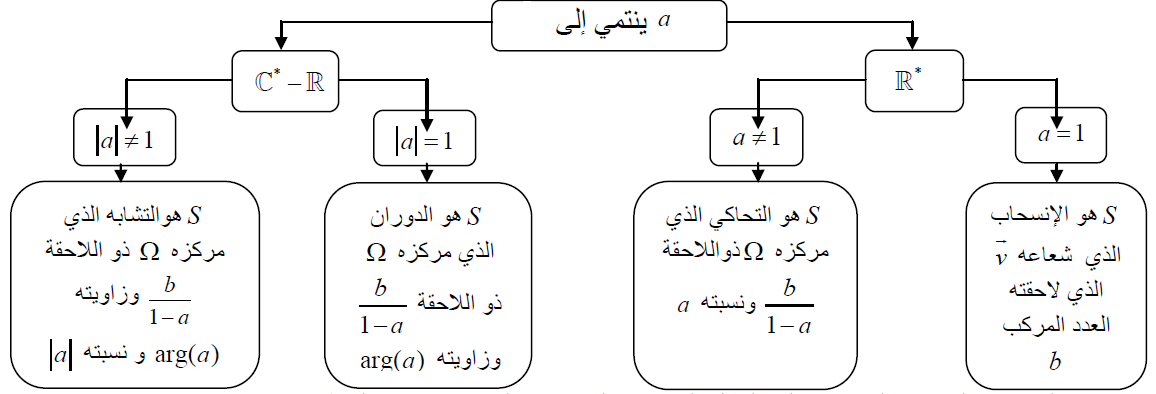
في المستوي المركب المنسوب إلى المعلم المتعامد المتجانس المباشر، نعتبر النقط
| العلاقة المركبة | المفھوم الھندسي |
| المسافة |
|
منتصف القطعة |
|
| قیس الزاویة |
|
| النقط على استقامة واحدة |
|
| النقط تنتمي إلى نفس الدائرة |
|
حیث |
; تنتمي إلى الدائرة التي مركزھا و نصف قطرھا |
; AB تنتمي إلى محور القطعة المستقیمة |
|
مثلث قائم الزّاویة في النقطة |
|
مثلث متساوي السّاقین في النقطة |
|
مثلث قائم الزّاویة ومتساوي الساقین في النقطة |
|
مثلث متساوي الأضلاع |









