القوة و الحركة المنحنية
يقذف لاعب كرة برجله , كما توضحه الصورة .
ما هو حسب رأيك ، مسار الكرة ؟
الكرة تصعد متبعة مسار منحني مسافة معينة ثم تنزل متبعة مسار منحني إلى الأرض .
اقترح تصوير متعاقبا لأوضاع الكرة خلال حركتها.
أنظر الشكل
هل تخضع الكرة لقوة خلال حركتها ؟
نعم حسب مبدأ العطالة ، الكرة حتما خاضعة لقوة لان المسار ليس مستقيما .
مثل بشعاع كيفي في مواضع مختلفة هذه القوة إن وجدت.
أنظر الشكل
نلاحظ من المسار مرحلتين : الصعود و النزول ، فالكرة لم تواصل صعودها دليل على وجود قوة مؤثرة تجذبها نحو الأسفل أي تعاكس حركتها ، أما خلال النزول فوجود هذه القوة بديهي وجهتها نحو الأسفل .
ندفع كرية معدنية صغيرة علي طاولة أفقيا ملساء , فتنطلق في اتجاه حافة الطاولة .
أكمل التصوير المتعاقب لحركة الكرية قبل مغادرة الطاولة .
ما هو نوع حركة الكرية على الطاولة ؟ لماذا ؟
حركة الكرية علي الطاولة مستقيمة منتظمة لان المسافات المتتالية المقطوعة في نفس المجالات الزمنية متساوية أي أن الحركة مستقيمة منتظمة و حسب مبدأ العطالة فالكرة تكون شبه معزولة .
ما هو مسارها بعد مغادرة الطاولة؟
بعد مغادرة الطاولة يكون مسار الكرية منحني .
أكمل التصوير المتعاقب لحركة الكرية بعد مغادرة الطاولة .
هل هناك قوة مطبقة على الكرة فوق الطاولة ؟
نعم , هناك قوتين تؤثران علي الكرية وهي قوة جذب الأرض للأجسام ويرمز لها بــ
هل هناك قوة مطبقة عليها بعد مغادرة الطاولة ؟ علل
نعم , بعد مغادرة الطاولة هناك قوة تؤثر على الكرية وهي قوة جذب الأرض للأجسام ويرمز لها بـ
لحساب قيمة السرعة اللحظية في الحركات المنحنية نعتمد علي تعريف السرعة المتوسطة
حيث :
لتحديد قيمة السرعةالمتوسطة بيانيا في حركة منحنية نعتمد علي مثال :
نعتبر التسجيل الممثل في الشكل المقابل , الممثل لحركة منحنية كيفية , حيث مواضع المتحرك
تفصلها مجالات زمنية متساوية
السرعة المتوسطة بين الموضعين
لأن المسافة
في هذه الحالة يمكن ان نكتب السرعة المتوسطة بين
بهذه الطريقة يمكن تحديد بيانيا قيمة السرعة المتوسطة
في مثالنا هذا :
- نقيس بالمسطرة طول الوتر ثم نحوله إلى الطول الحقيقي بالاعتماد علي سلم الرسم .
- نحسب قيمة السرعة المتوسطة بالعلاقة :
بالمقارنة مع حساب السرعة اللحظية في الحركة المستقيمة و بما أن المجال الزمني
ونمثلها بشعاع
- مبدأه .
- حامله مماسي للمسار في .
- جهته هي جهة الحركة .
- قيمته :
لتحديد عمليا شعاع تغير السرعة في الحركة المنحنية , نعتمد على الخطوات المتبعة فى حالة الحركات المستقيمة .
نستعين بالتسجيل الممثل فيى الشكل المقابل , حيث مواضع المتحرك تفصلها مجالات زمنية متساوية
لتحديد شعاع تغير السرعة
- نعتبر الموضعين ,,المجاورين للموضع المعتبر,و نمثل فيهما شعاعي السرعة اللحظيةو, على الترتيب باستعمال سلم تمثيل السرعة .
- نعتبر ان شعاع تغير السرعة في الموضعيساوي الفرق الشعاعي بين شعاعي السرعةو, أي أن :
-
تمثيل شعاع تغير السرعة
في الحركة المنحنية يتم كمايلي :
- نختار نقطة كيفية 0 خارج التسجيل .
- انطلاقا من هذه النقطة 0 نرسم شعاعا مسايرا للشعاع.
- انطلاقا من هذه النقطة 0 نرسم شعاعا مسايرا للشعاع.
- نرسم الشعاع , بحيث تكون بدايته في نهايةو نهايته في نهايةبهذا الترتيب,
- بما أن ,يسايران,على الترتيب , فانيساير.
تكون إذا خصائص الشعاع
- بدايته: الموضع المعتبر
- حامله : موازي لحامل
- جهته : هي جهة
- قيمته : تساوي طويلة المقاسة بيانيا على الرسم باعتماد سلم تمثيل السرعات .
ندفع كرة صغيرة على سطح طاولة أفقية ملساء, فتتجه نحو الحافة لتنطلق في الهواء حتى تسقط على سطح الأرض وفق مسار منحني, يمثل الشكل الآتي تسجيلا للأوضاع المتتالية لمركز الكرة خلال حركتها .
- انقل على ورق شفاف هذا التسجيل :
- حركة الكرة على الطاولة :
- ما هو نوع حركة الكرة على الطاولة ؟
بواسطة المسطرة نقيس المسافات بين كل موضعين متتاليين فنجدها متساوية ومنه نستنتج أن الحركة مستقيمة منتظمة .
- مثل شعاع السرعة اللحظية في الموضع باختيار سلم مناسب .
- نقيس طول المسافة فنجده :على الوثيقة وباختيار سلم المسافات :
- نحسب السرعة في الموضع:
- تمثيل شعاع السرعة اللحظية في الموضع باختيار السلم التالي
- نرسم شعاع السرعة اللحظية في الموضع بطولعلى الرسم
- ما هي خصائص شعاع السرعة اللحظية في الموضع الذي يوافق لحظة مغادرتها الطاولة ؟ مثله على الرسم .
خصائص شعاع السرعة اللحظية في الموضع
اللحظية نفس الخصائص في جميع النقاط ، ومنه :
-
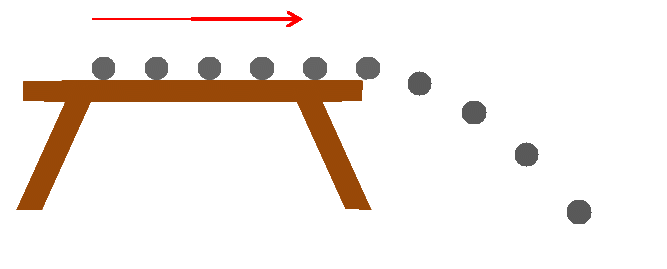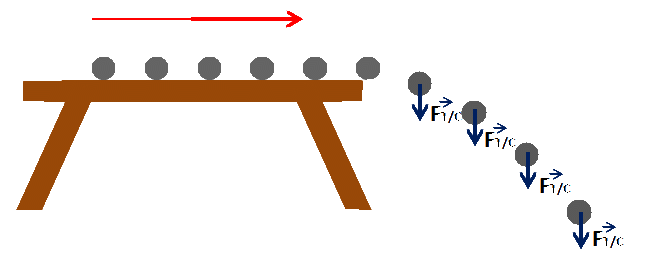
حركة الكرة بعد مغادرتها الطاولة :
أحسب قيم السرعة اللحظية
نستعين بطريقة تحديد السرعة اللحظية في الحركة المنحنية المذكورة سابقا ونملأ الجدول التالي:
مثل أشعتها على الرسم, باستعمال نفس السلم السابق, ماذا تلاحظ ؟
- نرسم أشعة السرعة من خلال أطوالها المحسوبة في الجدول .
- نلاحظ أن أشعة السرعة قيمتها تزداد و جهتها تتغير وتنحني تدريجيا في اتجاه حركة السقوط .
حدد بيانيا أشعة السرعة
- نحصل على قيم أشعة تغير السرعة بقياس طولها على الشكل .
- نلاحظ أن قيم أشعة تغير السرعة تقريبا متساوية, حواملها كلها شاقولية ولها نفس الجهة وكلها تتجه نحو الأرض.
ماذا تستنتج عن القوة المطبقة على الكرية ؟
بما أن خصائص شعاع تغيير السرعة
- لشعاع القوة وشعاع تغير السرعةنفس الحامل وهو شاقولي .
- لشعاع القوة وشعاع تغير السرعةنفس الجهة وهي نحو مركز الأرض .
- قيمة ثابتةقيمةثابتة.
مثلها بلون آخر على نفس الرسم في المواضع
نمثل على الشكل السابق أشعة القوة المطبقة بسهم حامله شاقولي موجه نحو مركز الأرض بأطوال متساوية.
ما هو مصدر هذه القوة ؟ اشرح .
- نعلم من حياتنا اليومية أن سقوط كرية في أي موضع من سطح الأرض دون سرعة ابتدائية يكون شاقوليا , ونعلم أن شاقول المكان يمر من مركز الأرض , إذن القوة المطبقة على الكرية متجهة دوما نحو مركز الأرض ونسمي هذه القوة قوة جذب الأرض للكرية, أو قوة تأثير الأرض على كرية ونرمز لها بالرمز .
- شعاع القوة هو نفسه قيمة وجهة في كل المواضع لأن مصدرها هو نفسه وهو الأرض .
- في مثالنا , المسار منحني وليس شاقولي لأنه توجد سرعة ابتدائية أفقية ، فقوة الأرض هي التي سببت في تغيير منحنى شعاع السرعة .
أرفق الرسم بمعلم
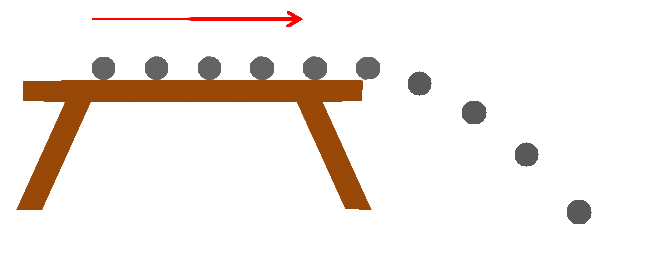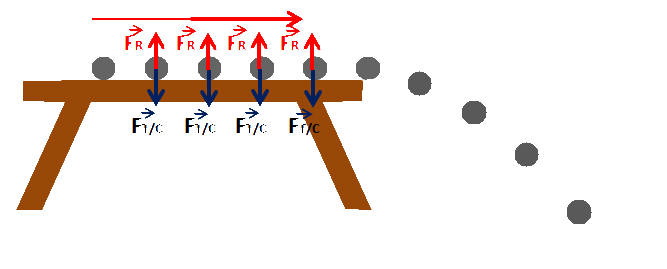
قارن المسافات المتتالية للمقطوعة وفق المحور
نلاحظ على الشكل أن المسافات المتتالية المقطوعة وفق المحور
قارن قيمة السرعة وفق المحور
نلاحظ على الشكل أن المسافات المتتالية المقطوعة وفق المحور
ما هو أثر القوة المطبقة على الكرة على حركتها وفق المحور
بما أن الحركة مستقيمة منتظمة وفق المحور
أي وفق المحور
قارن المسافات المتتالية المقطوعة وفق المحور
نلاحظ على الشكل أن المسافات المتتالية المقطوعة وفق المحور
حدد قيمة تغير السرعة وفق هذا المحور ، ماذا تلاحظ ؟
- لإيجاد قيمة تغير السرعة وفق المحور نحسب أولا المسافات على هذا المحور التي تسمح بحساب قيم السرع اللحظية ثم نستنتج قيم تغير السرعة وفق المحور.
- نستعين بطريقة تحديد السرعة اللحظية في الحركات المستقيمة المذكورة سابقا ونملأ الجدول التالي :
قارن هذه القيمة مع طويلة شعاع تغير السرعة المحددة سابقا في الدراسة الشعاعية .
نلاحظ أن قيمة تغير شعاع السرعة وفق المحور
دراسة حركة مقذوف أفقيا تتم على محورين
- وفق المحور : الحركة مستقيمة منتظمة وتأثير القوة المطبقة على الكرة يكون معدوما.
- وفق المحور : الحركة مستقيمة متسارعة بانتظام ويخضع الجسم لقوة ثابتة وهي قوة جذب الأرض للأجسام.
- نسمي "مدى القذف" البعد الأفقي الذي يفصل موضع القذف عن موضع سقوط الكرية على الأرض .
- حقق عمليا التجربة المدروسة سابقا في الشكل المقابل بدفع كرية بالأصبع على طاولة أفقية.
- راقب حركة الكرية منذ مغادرتها الطاولة ، أعد العملية ثلاث مرات مغيرا كيفية الدفع لتنتقل الكرية على الطاولة بسرعات مختلفة القيمة في كل مرة .
مقارنة الحركات
مثل كيفيا على الرسم شكل مسار الكرية في حالات تغير السرعة الابتدائية مع تعليم المواضع المتتالية لمركز الكرية بنقاط على هذه المسارات باعتبار فترة زمنية كيفية
نضع فوق الطاولة الأولى طاولة أخرى صغيرة لنقذف منها الكرية. نمثل المسارات المختلفة للكرية حسب سرعة قذفها, حيث نلاحظ :
- الحالة (1) : السرعة الابتدائية للكرية معدومة تكون في حالة سقوط حر .
- الحالات (4)(3)(2) : يكون للكرية سرعة ابتدائية أفقية متفاوتة القيمة .
نلاحظ أن مدى القذيفة في هذه الحالة يتزايد إلى أن تسقط الكرية خارج حدود الطاولة وهي في كل الحالات خاضعة لقوة جذب الأرض لها فهي تتجه دوما نحو الأرض.
بماذا يتعلق المدى في هذه التجربة ؟
يتعلق المدى في هذه التجربة فقط بالسرعة الابتدائية حيث عند انعدام السرعة الابتدائية ينعدم المدى فنحصل على حركة سقوط حر.
في رأيك هل الكرية خاضعة لنفس القوة في الحالات الأربع ؟
نعم الكرية خاضعة لنفس القوة في الحالات الأربع : حيث في الحالة الأولى (1) عند انعدام السرعة الابتدائية تكون الحركة هي حركة سقوط حر التي درسناها سابقا حيث يكون المسار شاقوليا والقوة المطبقة وجدناها هي قوة جذب الأرض أما الحالات (2)(3)(4) : للكرية سرع ابتدائية متفاوتة
كل جسم يقذف بسرعة ابتدائية أفقية من ارتفاع
نريد دراسة حركة كرة يقذفها لاعب برجله, حيث تطلق بسرعة ابتدائية , نعطي في الشكل المقابل التسجيل الممثل لمواضع الكرة خلال فترات زمنية متساوية .
كيف يتغير شعاع السرعة اللحظية من موضع لآخر ؟ مثله في ثلاث مواضع متتالية من مرحلة الصعود, ثم في ثلاث مواضع متتالية من مرحلة النزول .
لحساب قيمة السرعة اللحظية
نستعين بطريقة تحديد السرعة اللحظية في الحركة المنحنية المذكورة سابقا ونملأ الجدول التالي :
مثل أشعتها على الرسم باختيار سلم مناسب , ماذا تلاحظ ؟
نرسم أشعة السرعة من خلال أطوالها المحسوبة في الجدول.
نلاحظ أن أشعة السرعة تتناقص في مرحلة الصعود وكذا جهتها تتغير أما في مرحلة النزول فقيمتها تزداد وحواملها تنحني في اتجاه السقوط
ما نوع الحركة في مرحلة الصعود وما نوعها في مرحلة النزول ؟ علل.
- مرحلة الصعود : حركة منحنية متباطئة لأن السرعة قيمتها تتناقص.
- مرحلة النزول : حركة منحنية متسارعة لأن السرعة قيمتها تزداد.
أرسم مسار الكرة واستنتج أعلى موضع تبلغه. هل هذا الموضع ممثل في الوثيقة ؟ ناقش.
مسار الكرة ممثل على الشكل السابق وأعلى موضع تبلغه هو
حدد خصائص شعاع تغير السرعة في المرحلتين. ماذا تستنتج ؟
نحصل على قيم أشعة تغير السرعة
ما هي القوة المطبقة على الكرة خلال حركتها ؟ مثلها كيفيا في كل المواضع التي مثل فيها شعاع السرعة. علل.
القوة المطبقة على الكرية متجهة دوما نحو مركز الأرض.
نسمي هذه القوة قوة جذب الأرض للكرية , أو قوة تأثير الأرض على الكرية ونرمز لها بالرمز
شعاع القوة هو نفسه قيمة وجهة في كل المواضع لأن مصدرها هو نفسه وهو الأرض .
قارن حامل القوة مع جهة شعاع السرعة في كل هذه المواضع . ماذا تستنتج ؟
حامل شعاع القوة مختلف عن حامل شعاع السرعة في كل هذه المواضع. نستنتج أن للقوة تأثير على مسار الحركة.
قارن جهتها مع جهة شعاع السرعة في كل هذه المواضع. ماذا تستنتج ؟
جهة القوة مختلف عن جهة شعاع السرعة في كل هذه المواضع. نستنتج أن للقوة تأثير على جهة الحركة.
ما هي الزاوية التي يصنعها حامل شعاع القوة وحامل شعاع السرعة في المواضع المدروسة(منفرجة - حادة - قائمة) ؟
- مرحلة الصعود : حامل القوة يصنع مع حامل شعاع السرعة في كل هذه المواضع زاوية منفرجة
- عند الذروة : حامل القوة يصنع مع حامل شعاع السرعة زاوية قائمة.
- مرحلة النزول : حامل القوة يصنع مع حامل شعاع السرعة في كل هذه المواضع زاوية حادة .
كيف تتغير هذه الزاوية خلال الحركة ؟
تتغير هذه الزاوية خلال الحركة ابتداءا من منفرجة ثم قائمة ثم تصبح حادة.
حلل في المواضع السابقة, باستعمال الألوان, شعاع السرعة
قارن حامل شعاع القوة المطبقة على الكرة مع حاملي المركبتين
مرحلة الصعود أو النزول :
- حامل شعاع القوة المطبقة على الكرة عمودي على حامل المركبة في كل لحظة .
- حامل شعاع القوة المطبقة على الكرة منطبق على حامل المركبة في كل لحظة .
كيف تتغير قيمة المركبتين
- مرحلة الصعود : - المركبة دائما ثابتة وفي كل لحظة ومتناقصة.
- مرحلة النزول : - المركبة دائما ثابتة ومتزايدة.
هل تتغير جهة المركبتين في مرحة الصعود ؟ وفي مرحلة النزول ؟
- مرحلة الصعود : جهة المركبة لا تتغير وفي كل لحظة و جهة المركبةكذلك لا تتغير وهي نحو الأعلى.
- مرحلة النزول : جهة المركبة لا تتغير وفي كل لحظة و جهة المركبةكذلك لا تتغير وهي نحو الأسفل.
ماذا تستنتج عن أثر القوة على المركبة
أثر القوة على المركبة
ماذا تستنتج عن أثر القوة على المركبة
أثر القوة على المركبة
ماذا تستنتج عن أثر القوة على المركبة
أثر القوة على المركبة
ماذا يحدث للمركبة
عند مرور الكرة من أعلى موضع تشغله تنعدم المركبة
استنتاج شعاع السرعة في أعلى موضع تبلغه الكرة ومثله .
شعاع السرعة في أعلى موضع تبلغه الكرة حامله منطبق على المحور
شعاع السرعة في أعلى موضع تبلغه الكرة منطبق على المركبة
ماذا تستنتج عن أثر شعاع القوة على شعاع السرعة عندما يكون حامليهما متعامدين دوما ؟ (في كل لحظة) ما طبيعة الحركة في هذه الحالة وما نوعها ؟
لا يوجد أثر لشعاع القوة على قيمة شعاع السرعة بل تغير جهتها فقط فعندما يكون حامليهما متعامدين دوما وفي هذه الحالة طبيعة الحركة تكون منتظمة وبما أن المسار منحني (لأن الجهة تتغير) فنقول عن الحركة أنها دائرية منتظمة.
ماذا تستنتج عن أثر القوة المطبقة على تغيرات السرعة اللحظية حسب الزاوية
أثر القوة المطبقة على تغيرات السرعة اللحظية حسب الزاوية
- عندما أو: تتغير قيمة السرعة دون تغير المنحى (حركة مستقيمة) .
- وعندما : تغير في المنحى دون التغير في القيمة (حركة دائرية) .
- نستنتج أن لزاوية القذف تأثير على الحركة :
- منفرجة : تغير منحى شعاع السرعة مع تناقص طويلته.
- حادة : تغير منحى شعاع السرعة مع تزايد طويلته.
-
- وتمهد هذه الدراسة حالة الحركة الدائرية المنتظمة أين الزاوية بين شعاعي القوة والسرعة تساوي دائما
دائما .
نقول عن حركة جسم أنها دائرية منتظمة إذا كان مسارها دائريا وسرعة المتحرك ثابتة القيمة ومتغيرة المنحى والجهة خلال الحركة ، أي أن شعاع السرعة
إن شعاع القوة
للتأكد تجريبيا من خصائص القوة في الحركة الدائرية المنتظمة, نقوم بتسجيل الحركة التالية :
- نستعمل "جسما محولا ذاتيا" وهو قرص تحتوي قاعدته السفلية ثقوبا صغيرة ويبث فيه هواء مضغوط من الأعلى بحيث خروج الهواء المضغوط من الأسفل يكون "وسادة هوائية" بينه وبين الطاولة الأفقية التي تحمله ، ذلك ما يسمح له بالتحرك دون احتكاك عليها.
- نشد القرص بخيط رفيع عديم الامتطاط طوله إلى نقطةعلى حافة الطاولة ثم نقذفه بمسطرة.
- يرفق القرص والطاولة بتجهيز يترك آثار مواضع القرص على ورقة خلال فترات زمنية متساوية.
- نعطي في الشكل الآتي تسجيلا لآثار مركز القرص خلال حركته .
تحليل تجربة :
اعتمادا على هذا التسجيل برهن أن الحركة دائرية منتظمة .
أرسم أشعة السرعة في المواضع
نستعين بطريقة تحديد السرعة اللحظية في الحركة المنحنية المذكورة سابقا ونملأ الجدول التالي :
مثل أشعتها على الشكل, باختيار سلم مناسب . ماذا تلاحظ ؟
نرسم أشعة السرعة من خلال أطوالها المحسوبة في الجدول : نلاحظ أن أشعة السرعة ثابتة القيمة ومتغيرة المنحى.
حدد خصائص شعاع تغير السرعة
نلاحظ في الشكل أن شعاع تغير السرعة
- كيف تكون حركة هذا القرص المقذوف في حالة غياب الخيط ؟ علل.
- ما هي حالة القرص إذا انقطع الخيط فجأة ؟ علل .
في حالة غياب الخيط أو انقطاعه فجأة فإن القرص يصبح غير خاضع لأي قوة , أي معزول, فحسب مبدأ العطالة القرص يواصل حركته بحركة مستقيمة منتظمة بنفس السرعة التي كان يملكها لحظة انقطاع الخيط .
أول من فسر دوران القمر حول الأرض العالم اسحاق نيوتن (Isaac Newton) الذي بنى نظرية الجذب العام من ملاحظاته الحركة الكواكب واعتمادا على أسلافه غاليلي Gallilée وكيبلر Kepler ، إذ يحكى أن الفكرة التي سمحت له بربط حركة الأجسام على الأرض بحركة الكواكب هو سقوط تفاحة من شجرة كان جالسا بجوارها ، يقال أن نيوتن تساءل عن سبب سقوط التفاحة على الأرض وعدم سقوط القمر عليها ، فوصل إلى نتيجة أن التفاحة تسقط من ارتفاع معين بدون سرعة ابتدائية , فتكون حركتها مستقيمة متسارعة نحو الأرض وتحت تأثير قوة جذب الأرض لها , أما القمر أيضا يخضع لقوة جذب الأرض ولكنه متحرك بسرعة معينة فهو في حالة سقوط دائم نحو الأرض مثل التفاحة, لكن سرعته العمودية على منحى شعاع القوة تكسبه حركة دائرية منتظمة.
كيف يمكن أن نجعل من كرتنا قمرا اصطناعيا يدور حول الأرض ؟
من أجل ذلك نتخيل كما فعله نيوتن في عهده, أننا نقذف من أعلى جبل هذه الكرية بسرعة أفقية متفاوتة القيمة, مثلما حققناه في التجربة السابقة.
- إذا كانت سرعة القذف كافية بحيث تكون لها حركة دائرية نصف قطرها أكبر من نصف قطر الأرض تصبح قمرا اصطناعيا يدور حولها.
- حركة القمر حول الأرض : لا يسقط القمر على الأرض لأن له سرعة كافية للمحافظة على مداره, يقال عن القمر أنه في سقوط دائم على الأرض دون لمسها.









