مهتز ميكانيكي عبارة عن جسم صلب
عند اللحظة
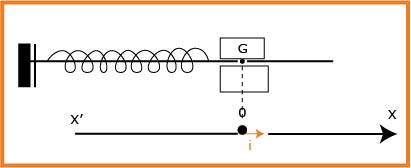
بواسطة تجهيز خاص يمكن متابعة تغيرات الفاصلة
I- الدراسة البيانية :
1- ما هو نمط الاهتزازات؟
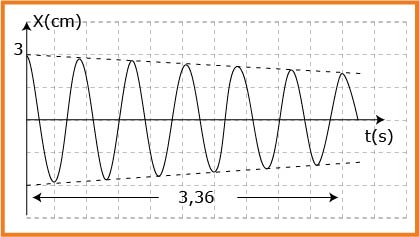
نمط الاهتزازات : حرة متخامدة و النظام المتحصل عليه شبه دوري .
2- أحسب قيمة شبه الدور للاهتزازات ؟
من البيان نلاحظ :
و منه
3- ما هي قيمة الفاصلة
في اللحظة
في اللحظة
في اللحظة
II- الدراسة الطاقوية :
1- أكتب عبارة الطاقة الكلية للجملة (نابض،جسم
الطاقة الكلية للجملة (نابض ، جسم
2- أحسب قيمة الطاقة الكلية للمهتز عند اللحظات السابقة .
نلاحظ أنه في هذه اللحظات تكون
في اللحظة
في اللحظة
في اللحظة
3- قارن بين القيم المتحصل عليها ، ما هو سبب التغير في الطاقة الكلية ؟
نلاحظ أن قيمة الطاقة تتناقص مع الزمن و ذلك بسبب وجود قوى الإحتكاك
4- أحسب سرعة مرور الجسم لأول مرة من وضع التوازن .
نلاحظ من البيان أن أول مرور بوضع التوازن يكون في الاتجاه السالب ومنه السرعة عظمى وسالبة.
و بما أن مقدار تناقص الطاقة خلال زمن قصير يكون صغيرا جدا لذا يمكن اعتبار الطاقة ثابتة خلال هذه المدة
ومنه :
ينتج :
III- الدراسة النظرية: (نهمل الاحتكاك)
1- مثل القوى المؤثرة على الجسم
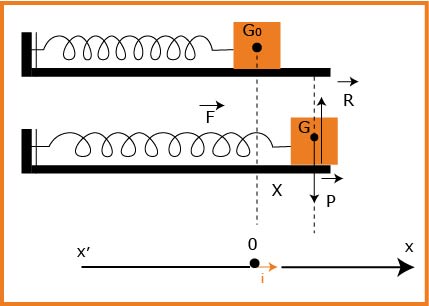
2- مرجع الدراسة أرضي غاليلي ، بتطبيق قانون نيوتن الثاني على الجملة (جسم) بين أن المعادلة التفاضلية للحركة هي من الشكل التالي:
بتطبيق قانون نيوتن الثاني على الجملة (جسم) ينتج
بالإسقاط الجبري على المحور
لدينا
و هي المعادلة التفاضلية المطلوبة .
3- عبر عن
لدينا :
و منه
نبين أن
بالتعويض في المعادلة التفاضلية نجد :
لدينا :
بالتعويض نجد :
و بالتالي هذه المعادلة الزمنية هي حل للمعادلة التفاضلية السابقة
4- بين أن عبارة الدور الذاتي
5- أحسب قيمة
لدينا :
القيمتان
* الدقة في القياس
ومنه دقة القياس هي :








