الهندسة المستوية و الأشعة
متوازي الأضلاع هو رباعي حيث كلّ ضلعين متقابلين فيه متوازيان .
من أجل كل رباعي
- ومتناصفانتكافئ (متوازي الأضلاع)
- و) تكافئ (متوازي الأضلاع)
- وتكافئ (متوازي الأضلاع)
- وتكافئ (متوازي الأضلاع)
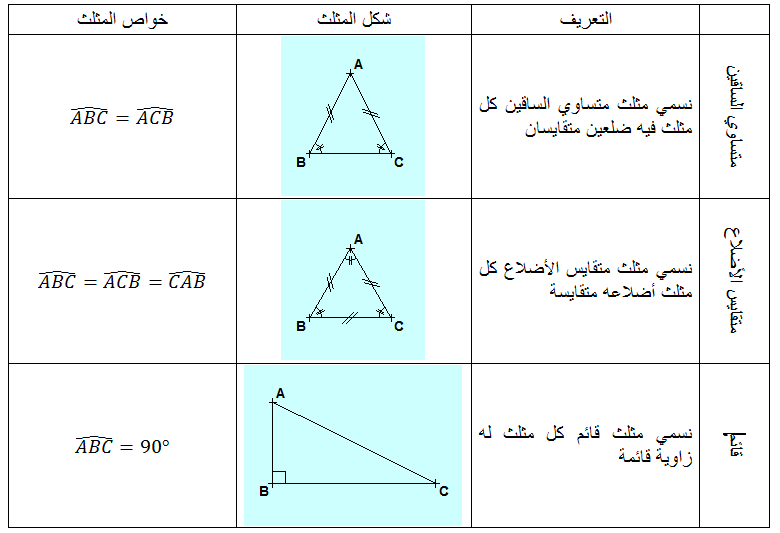

- إذا كان المثلث قائم فيفإن
- إذا كان في المثلث ،فإن المثلثقائم في
إذا كان المثلث
- نسمي جيب الزاوية العدد الحقيقيحيث

- نسمي جيب تمام الزاوية العدد الحقيقيحيث

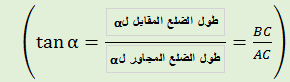
- نسمي ظل الزاوية العدد الحقيقيحيث
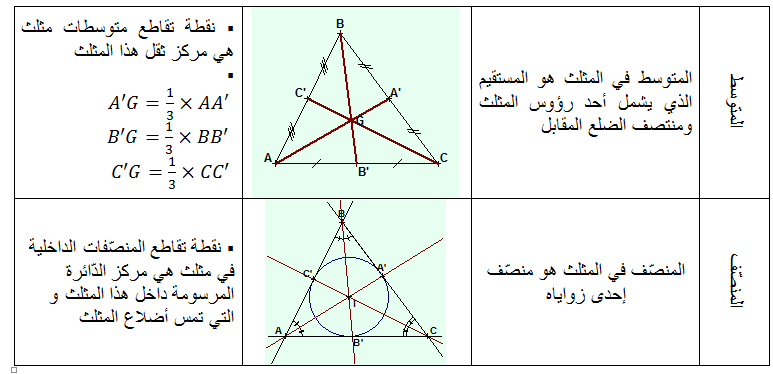
إذا كان لدينا مستقيمان متقاطعان في نقطة
و إذا كان
إذا كانت
و إذا
- تسمّى قطرا ونسمي كلّ منوترا الدائرة
- النقطتين والمتمايزتان تعيّنان على الدائرةقوسين نرمز إلى كلّ واحد منهما بالرمز
- نسمي المستقيم الذي يشترك مع الدائرةفي نقطة واحدة : مماسا للدائرةعند النقطة
- الزاوية رأسهاتسمى زاوية مركزية و نقول عنها أنها تحصر القوسمركز الدائرة
- الزاوية رأسها الدائرةتسمى زاوية محيطية و نقول عنها أنها تحصر القوس
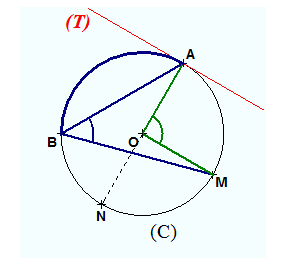
في كلّ دائرة، الزّاوية المركزيّة تساوي ضعف الزّاوية المحيطية التي تحصر معها نفس القوس
- في الدائرة، الزّوايا المحيطية التي تحصر نفس القوس أو تحصر أقواس متقايسة فهي متقايسة
- إذا كانت قطرا للدائرةو كانتنقطة ثالثة من الدائرة (تختلف عنو تختلف عن) فإن المثلثقائم في
- تكون رؤوس الرباعي المحدّب من نفس الدائرة إذاو
- نقول عن مثلثين أنهما متقايسان إذا كانت أطوال أضلاعها متساوية مثنى مثنى
- إذا كان مثلثان متقايسان فإن زواياهما متقايسة مثنى مثنى
- إذا تقايست زاوية والضلعان اللذان يحصرانها من أحد مثلثين مع زاوية والضلعان اللذان يحصرانها من مثلث أخر
فإن هذان المثلثان متقايسان
- إذا تقايس ضلع والزاويتان المجاورتان له من مثلث مع ضلع والزاويتان المجاورتان له من مثلث لأخر فإن هذان
المثلثان متقايسان
- نقول عن مثلثين أنهما متشابهان إذا كانت زوايا أحدهما تساوي زوايا الأخر
- الأضلاع المتماثلة لمثلثان متشابهان متناسبة وهذا معناه أن
إذا كان المثلثان
- يتشابه مثلثان إذا تقايست زاويتين من أحدهما مع زاويتين من المثلث الثاني
- يتشابه مثلثان إذا تقايست زاوية من أحدهما مع زاوية من المثلث الثاني و كان طولا الضلعين الذين يحصران إحدى
هاتين الزاويتين متناسبين مع طولي الضلعين الذين يحصران الزّاوية الأخرى
- يتشابه مثلثان إذا كانت أطوال الأضلاع المتماثلة فيها متناسبة
نسمي نسبة تشابه هذان المثلثان العدد الحقيقي
نسمي التناظر بالنسبة للمستقيم
إذا كانت
إذا كانت
نسمي التناظر بالنسبة للنقطة
ونسمي النقطة الثابتة
نسمي الانسحاب الذي شعاعه
توجيه المستوي هو اختيار اتجاه واحد على كلّ دوائر هذا المستوي علما أن الاتجاه المباشر (أو الاتجاه الموجب) هو الاتجاه المعاكس لاتجاه حركة عقارب الساعة
نسمي الدوران الذي مركزه
نقول عن نقطة
- نسمي تقايس كلّ تحويل نقطي يحافظ على المسافات
- الانسحاب، التناظر المركزي، التناظر المحوري والدواران تقايسات
- لتقايسات تحافظ على الاستقامية معناه إذا كانت ثلاثة نقط من المستوي على استقامية فإنصورها على هذا الترتيب بتقايس تكون في استقامية
- صورة مستقيم بتقايس هو مستقيم
- صورة زاوية بتقايس هي زاوية تقايسها
- إختبارات
- 20
- الأجوبة الصحيحة
- False
- الأجوبة الخاطئة
- False
- مجموع النقاط
- False
المراتب الخمس الأولى في Quiz
- abdou gmd
- 500 نقطة
-

- رباب جعفري
- 381 نقطة
-

- Marwan Kharroubi
- 314 نقطة
-

- Mehdi Amireche
- 200 نقطة
-

- Derias Abdo
- 183 نقطة
-
- SALAH EDDINE SALAH
- 180 نقطة
-

- sasa nana
- 174 نقطة
-

- sabrina fettah
- 160 نقطة
-

- lilou lylia
- 157 نقطة
-

- snow blind
- 155 نقطة
-










