الجداء السلمي و تطبيقاته
نسمي الجداء السلمي للشعاعين
- إذاو
- إذاأو
- الجداء السلمي لشعاعين عدد حقيقي و ليس شعاع
- إذا وفقط إذا كان (ومتعامدان).
الحالة الأولى :إذا كان
في هذه الحالة الحداء السلمي معدوم والشعاعين متعامدان (نقبل اصطلاحا أن اشعاع المعدوم عمودي على أي شعاع)
و منه الملاحظة صحيحة
الحالة الثانية : إذا كان
(
(
- و هذا من أجل كل شعاع
في المستوي الموجه توجيها مباشرا ، وحدة الطول هي السنتيمتر
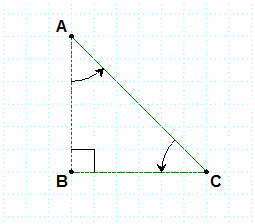
باستعمال مبرهنة بيتا قورس نحصل على
- و منه
منه
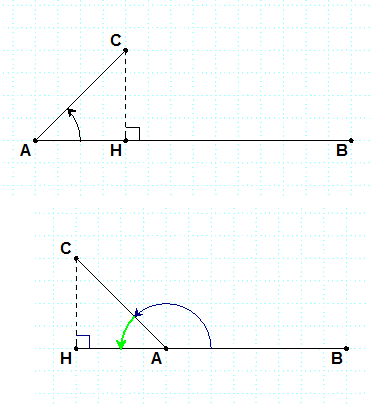
في الشكل الأول :
في الشكل الثاني :
و منه
في المثلث
و منه
من
إذا كانت
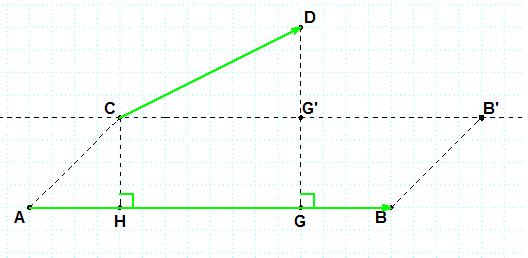
من أجل كل الأشعة
- و
و بما أن
و بما أن
------------------------------------------------------------------------
- إذا كان
و منه
- إذا كان
و منه
-------------------------------------------------------------------------------------------
علما أن
و منه من
المستوي الموجه توجيها مباشرا منسوب إلى المعلم المتعامد والمتجانس
إذا كانت
نعلم أن
- إذا كانت
(
--------------------------------------------------
- إذا كانت
فإن
- إذا كانت
فإن:
-----------------------------------------------------------------------
- المسافة بين النقطتين وهي
نقول عن الشعاع الغير معدوم
أنه شعاع ناظمي للمستقيم
المستوي منسوب إلى المعلم المتعامد و المتجانس
و ليكن
للمستقيم ذو الشعاع النظمي
معادلة من الشكل
و العكس صحيح
كل معادلة من الشكل
نعلم أن
و بما أن
في المستوي منسوب إلى المعلم المتعامد و المتجانس
و بما أن
معادلة الدائرة التي مركزها
في المستوي منسوب إلى المعلم المتعامد و المتجانس
نعلم أن من أجل كل نقطة
و تكافئ
معادلة الدائرة التي قطرها
معادلة دائرة علم قطرها أو علم مركزها و نصف قطرها هي من الشكل
و العكس خاطئ ، ليست كل المعادلة من الشكل
المستوي منسوب إلى المعلم المتعامد و المتجانس
نسمي المسافة بين النقطة
نرمز إلى هذه المسافة بالرمز:
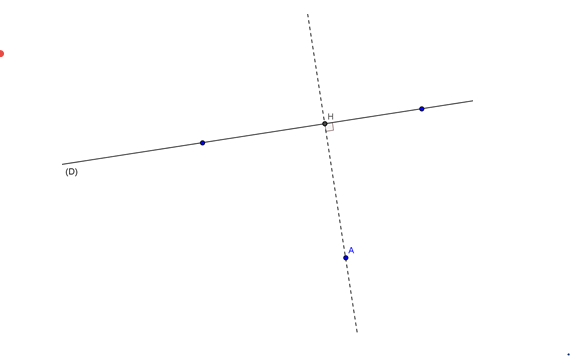
المستوي منسوب إلى المعلم المتعامد و المتجانس
إذا كان
ليكن
الشعاع ناظمي ل
لتكن
و بما أن
من
- إذا كانت النقطة منتصف القطعةفإن من أجل كل نقطةمن المستوي:
و منه
- إذا كان مثلث حيثووفإن:
- إذا كان مثلث حيثووفإن مساحة المثلثهيحيث :
- إذا كان مثلث حيثووفإن :
المستوي منسوب إلى المعلم المتعامد و المتجانس
نعتبر النقطتين
منه
نعلم أن إذا كانت
و منه
من
بالجمع
نضع
منه
بالطرح
بالجمع
بالطرح:
- إختبارات
- 20
- الأجوبة الصحيحة
- False
- الأجوبة الخاطئة
- False
- مجموع النقاط
- False
المراتب الخمس الأولى في Quiz
- اسماء رابية
- 200 نقطة
-

- خولة سرين
- 195 نقطة
-

- rokia rabia
- 180 نقطة
-

- mohe serir
- 177 نقطة
-

- nesrine fifi
- 172 نقطة
-

- bousseksou meli
- 167 نقطة
-

- La ByLkà
- 160 نقطة
-

- Hįčhęmøú Hįčhęm
- 152 نقطة
-
- ikram GH
- 149 نقطة
-

- amine Hazi
- 134 نقطة
-










